Simulation de Fluide en 200 Lignes de Code

8 minute(s) de lecture

La mécanique des fluides est une branche de la physique étudiée depuis longtemps par de nombreux scientifiques, que ce soit par Archimède, Newton, Bernoulli ou encore Lagrange. Elle permet de comprendre comment les fluides (les gaz et les liquides) se comportent et aide les ingénieurs à construire des turbines, prédire la météo et améliorer l’aérodynamisme des avions. Généralement, dans la vie de tous les jours il est difficiel de s’imaginer les trajectoire d’un fluide si ce n’est regarder l’eau qui coule de notre robinet. En cherchant un peu, on se rend compte que les trajectoires des fluides peuvent être assez chaotiques avec de nombreuses turbulences et vortex. Dans ce post, je vais simuler via les équations de la physique et visualiser comment un fluide réagit au clic de ma souris avec un petit code en Javascript. Pour se faire, je me suis grandement inspiré du travail de Matthias Müller et de sa vidéo ainsi que de son document 17-fluidSim.pdf qui décortique la magie derrière la mécanique des fluides numérique (CFD).

Les Équations de Navier-Stokes

Les équations de Navier-Stokes*régissent le comportement des fluides et décrivent leur comportements avec des termes aux dérivées partielles non linéaire. De nombreuses déclinaisons existe selon le cas qu’on étudie, ici j’utiliserais 2 équations princiaples : la conservation de la quantité de mouvement et la condition d’incompressibilité. La première correspond en fait à la 2ème loi de Newton $F = ma$ appliquée à un fluide. Si on note $u$ le champ de vitesse du fluide, $p$ la pression et les coefficients de densité $\rho$ et de viscosité $\nu$ alors on peut l’écrire de la façon suivante:

\[\underbrace{\frac{\partial \mathbf{u}}{\partial t}}_{\text{Accélération}} + \underbrace{(\mathbf{u} \cdot \nabla) \mathbf{u}}_{\text{Advection}} = \underbrace{-\frac{1}{\rho} \nabla p}_{\text{Gradient de Pression}} + \underbrace{\nu \nabla^2 \mathbf{u}}_{\text{Viscosité}} + \underbrace{\mathbf{f}}_{\text{Forces}}\]

La Variation Temporelle $\frac{\partial u}{\partial t}$ : C’est l’accélération “locale”. Elle décrit comment la vitesse en un point précis de la grille change d’un instant à l’autre. Si vous ne touchez à rien et que le fluide finit par s’immobiliser, c’est ce terme qui traduit cette évolution vers le repos.
L’Advection $(u \cdot \nabla) u$ : C’est le terme responsable du comportement chaotique et non-linéaire. Il décrit comment la vitesse du fluide se transporte elle-même à travers l’espace. C’est ce qui crée les tourbillons (vortex).
Le Gradient de Pression $-\frac{1}{\rho} \nabla p$ : Il garantit que le fluide est poussé des zones de haute pression vers les zones de basse pression. C’est le moteur qui “répare” le champ de vitesse pour le maintenir incompressible.
La Viscosité $\nu \nabla^2 u$ : Elle représente le “frottement” interne ou la diffusion de la quantité de mouvement. Un fluide très visqueux résiste au glissement de ses couches internes (comme le miel).
Les Forces Externes $f$ : Généralement la gravité. Dans notre demo, ça sera l’interaction avec l’utilisateur via la souris.

La seconde équation modélise la condition d’incompressibilité. Pour la fumée ou l’eau, on considère souvent que le fluide ne peut pas être compressé (son volume reste constant) :

\[\nabla \cdot \mathbf{u} = 0\]

Cette équation de divergence nulle signifie mathématiquement que tout ce qui entre dans une cellule de notre grille doit obligatoirement en ressortir. C’est la contrainte qui force le fluide à créer des courbes et des tourbillons plutôt que de simplement s’écraser et disparaitre contre un mur.

Modéliser le mouvement

Lors de la simulation de fluides, deux points de vue existent, chacun ayant sa propre manière d’interpréter le mouvement :

Approche Lagrangienne : on traite le fluide comme une collection de particules, on suit un ensemble de points individuellement s’entrechoquer au cours du temps. C’est intuitif, comme simuler un tas de billes.

Points Forts	Points Faibles
les frontières complexes et les éclaboussures sont gérées de façon naturelle et efficace. Puisque la masse est portée par les particules, elle est conservée par défaut.	garantir que le fluide ne se “comprime” pas (l’incompressibilité) nécessite des calculs de voisinage très coûteux, car il faut savoir quelles particules sont proches les unes des autres à chaque instant.

Approche Eulérienne : au lieu de suivre le mouvement, on fixe notre regard sur des points précis de l’espace. On divise le domaine en une grille (un peu comme les pixels d’une image) et on observe comment les propriétés (vitesse, pression, densité) évoluent dans chaque cellule.

Points Forts	Points Faibles
les calculs sont plus stable numériquement. Le calcul des gradients de pression et de la diffusion est beaucoup plus simple sur une structure fixe, ce qui permet de simuler facilement des fluides qui conservent un volume constant.	un phénomène de “dissipation numérique” (le fluide a tendance à devenir un peu trop visqueux ou flou avec le temps) peut avoir lieu si la résolution de la grille n’est pas assez fine.

Pour cette simulation, j’utiliserais l’approche Eulérienne car elle est souvent plus facile à gérer pour l’incompressibilité et produit de meilleurs résultats simuler la fumée. On peut obtenir des mouvements tourbillonnants comme les vortex si caractéristiques des gaz, tout en maintenant un rendu visuel lisse et continu, là où une approche par particules pourrait paraître “granuleuse”.

La Grille Décalée (Staggered Grid)

Une astuce clé dans la simulation Eulérienne est l’utilisation d’une grille décalée. Au lieu de stocker toutes les variables (pression, vitesse horizontale $u$, vitesse verticale $v$) au centre de chaque cellule, nous les décalons :

Pression ($p$) : Stockée au centre de la cellule $(i, j)$.
Vitesse Horizontale ($u$) : Stockée au centre des faces verticales de la cellule $(i+1/2, j)$.
Vitesse Verticale ($v$) : Stockée au centre des faces horizontales de la cellule $(i, j+1/2)$.

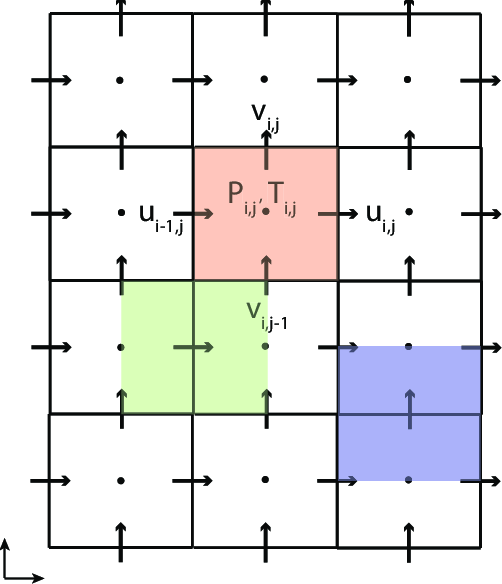
Diagramme de Grille Décalée
L'arrangement de la Grille Décalée

Cet arrangement évite les instabilités numériques (comme le problème du “damier”) et rend le calcul des gradients et de la divergence beaucoup plus précis. Par exemple, la dérivée $\frac{\partial p}{\partial x}$ est naturellement définie à l’emplacement de $u$.

L’Algorithme

Nous résolvons les équations en utilisant le splitting d’opérateur, ce qui signifie que nous traitons chaque terme de l’équation de Navier-Stokes séquentiellement. La boucle de simulation se compose de trois étapes principales, répétées à chaque image :

Forces Externes : $\mathbf{u} \leftarrow \mathbf{u} + \mathbf{f} \Delta t$
Projection (Incompressibilité) : Résoudre $\nabla \cdot \mathbf{u} = 0$ en ajustant la pression.
Advection : Déplacer le fluide (et le champ de vitesse lui-même) le long du flux.

1. Forces Externes

C’est la partie la plus simple. Nous ajoutons simplement la gravité à la composante verticale de la vitesse.

integrate(dt, gravity) {
    var n = this.numY;
    for (var i = 1; i < this.numX; i++) {
        for (var j = 1; j < this.numY-1; j++) {
            if (this.s[i*n + j] != 0.0 && this.s[i*n + j-1] != 0.0)
                this.v[i*n + j] += gravity * dt;
        }
    }
}

2. Projection (Rendre le tout Incompressible)

Les fluides réels comme l’eau sont incompressibles. Dans une grille, cela signifie que la divergence du champ de vitesse doit être nulle ($\nabla \cdot \mathbf{u} = 0$).

Si une cellule a un flux net entrant (divergence positive), la pression augmente, poussant le fluide vers l’extérieur. Nous résolvons l’équation de Poisson pour la pression :

\[\nabla^2 p = \frac{\rho}{\Delta t} \nabla \cdot \mathbf{u}\]

Une fois que nous avons la pression, nous mettons à jour les vitesses pour annuler la divergence :

\[\mathbf{u}_{new} = \mathbf{u} - \frac{\Delta t}{\rho} \nabla p\]

Nous utilisons une méthode itérative appelée Gauss-Seidel avec Sur-Relaxation (SOR) pour accélérer la convergence.

solveIncompressibility(numIters, dt) {
    // ... setup ...
    for (var iter = 0; iter < numIters; iter++) {
        for (var i = 1; i < this.numX-1; i++) {
            for (var j = 1; j < this.numY-1; j++) {
                // ... check boundaries ...

                // Calculer la divergence (flux sortant net)
                var div = this.u[(i+1)*n + j] - this.u[i*n + j] +
                          this.v[i*n + j+1] - this.v[i*n + j];

                // Calculer la correction de pression
                var p = -div / s;
                p *= scene.overRelaxation; // SOR pour la vitesse
                this.p[i*n + j] += cp * p;

                // Mettre à jour les vitesses
                this.u[i*n + j] -= sx0 * p;
                this.u[(i+1)*n + j] += sx1 * p;
                this.v[i*n + j] -= sy0 * p;
                this.v[i*n + j+1] += sy1 * p;
            }
        }
    }
}

3. Advection

L’advection est le processus de transport de quantités (comme la densité de fumée ou la température) avec l’écoulement du fluide. De manière cruciale, le champ de vitesse s’advecte aussi lui-même !

Nous utilisons un schéma Semi-Lagrangien. Pour trouver la nouvelle valeur d’une quantité $q$ à un point de la grille $\mathbf{x}$, nous traçons le vecteur vitesse en arrière dans le temps pour trouver d’où venait la particule de fluide ($\mathbf{x}_{prev}$), et échantillonnons la valeur à cette position précédente.

\[\mathbf{x}_{prev} = \mathbf{x} - \mathbf{u}(\mathbf{x}) \Delta t\] \[q_{new}(\mathbf{x}) = q_{old}(\mathbf{x}_{prev})\]

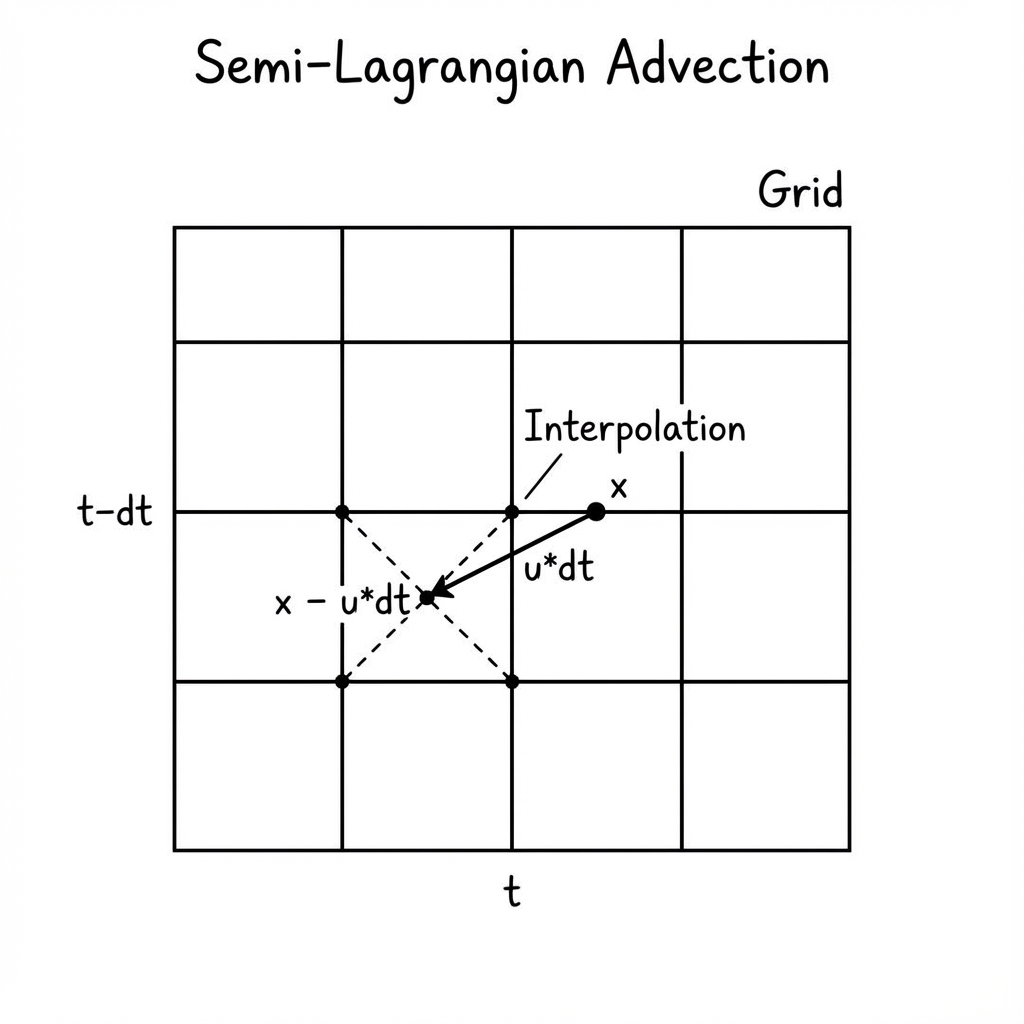
Schéma d'Advection Semi-Lagrangienne

advectVel(dt) {
    this.newU.set(this.u);
    this.newV.set(this.v);

    // ... boucle sur la grille ...
        // Tracer la position en arrière : x_prev = x - u * dt
        var x = i*h;
        var y = j*h + h2;
        var u = this.u[i*n + j];
        var v = this.avgV(i, j);
        x = x - dt*u;
        y = y - dt*v;

        // Échantillonner la valeur à la position précédente
        u = this.sampleField(x,y, U_FIELD);
        this.newU[i*n + j] = u;
    // ... fin de boucle ...

    this.u.set(this.newU);
    this.v.set(this.newV);
}

Conclusion

Avec seulement ces trois étapes — Forces, Projection et Advection — vous pouvez créer une simulation de fluide étonnamment réaliste. Le code est compact, efficace et s’exécute directement dans le navigateur.

Cette implémentation est un excellent point de départ. À partir de là, vous pouvez ajouter des obstacles, de la viscosité, différentes conditions aux limites, ou même l’étendre à la 3D !

Démo Interactive

Voici une implémentation complète en JavaScript que vous pouvez essayer directement. Cliquez et maintenez pour ajouter de la fumée :

Viscosité 0.00

Rayon 0.05

Dissipation 0.99

Julien Guégan