Objet Fractal : Dimension, Auto-similarité, Infini

Elles sont présentes dans les forêts tropicales, à la pointe de la recherche médicale, dans les films et partout où reigne la communication sans fil. Ce mystère de la nature a enfin été percé à jour. “Bon sang ! Mais c’est bien sûr !”. Peut-être n’avez vous jamais entendu parler de ces formes étranges, pourtant elles sont partout autour de vous. Leur nom : les fractales.

reportage ARTE – à la recherche de la dimension cachée

Introduction

Comme vous l’aurez compris si vous avez regardé l’excellent documentaire d’ARTE présenté ci-dessus, les fractales sont des objets géométriques infiniment morcelés qui ont la particularité de présenter des structures similaires à toutes les échelles. Ce type de géométrie permet de modéliser avec de simples formules récursives des figures infiniment complexes mais aussi de décrire des phénomènes naturels (motifs des flocons, chemin pris par la foudre, forme d’un choux de romanesco, structure des poumons …) et de trouver des applications dans des domaines technologiques (antennes, transistors, génération graphique de paysages …).

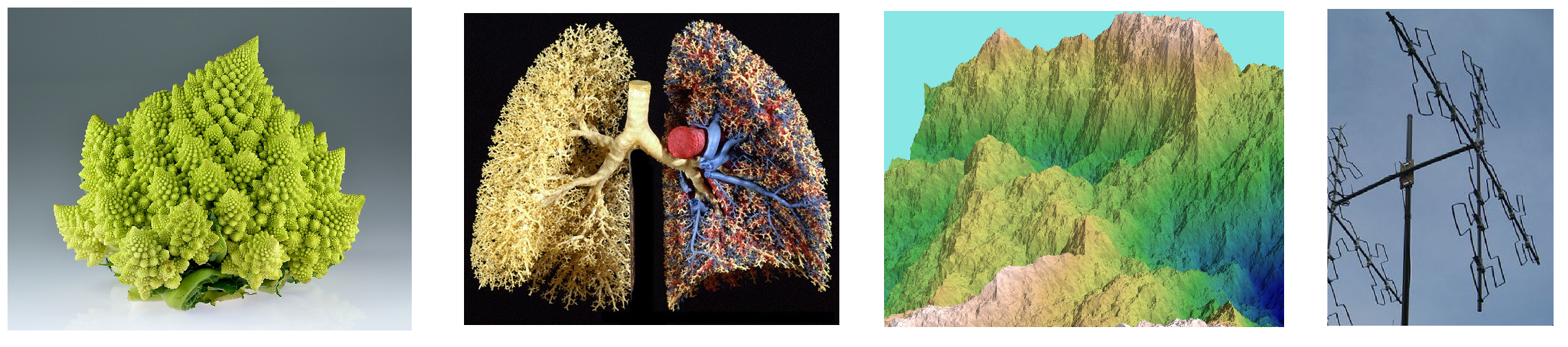
Note: Les fractales qu’on trouve dans la nature sont des approximations finies des vrais objets mathématiques.

Les fractales sont notamment caractérisées par la notion contre intuitive de dimension non entière. En effet, on peut définir une régle générale de mise à l’échelle qui relie la mesure $N$, un facteur d’échelle $\varepsilon$ et la dimension $D$ :

\[N = \varepsilon^{-D}\]

Par exemple, pour une figure géométrique usuelle comme le carré, sa dimension est $D=2$ et si on le subdivise en $3$ son aire est $N=9$, on a bien $9=\frac{1}{3}^{-2}$. On peut appliquer ce même raisonnement pour un cube ou même une ligne.

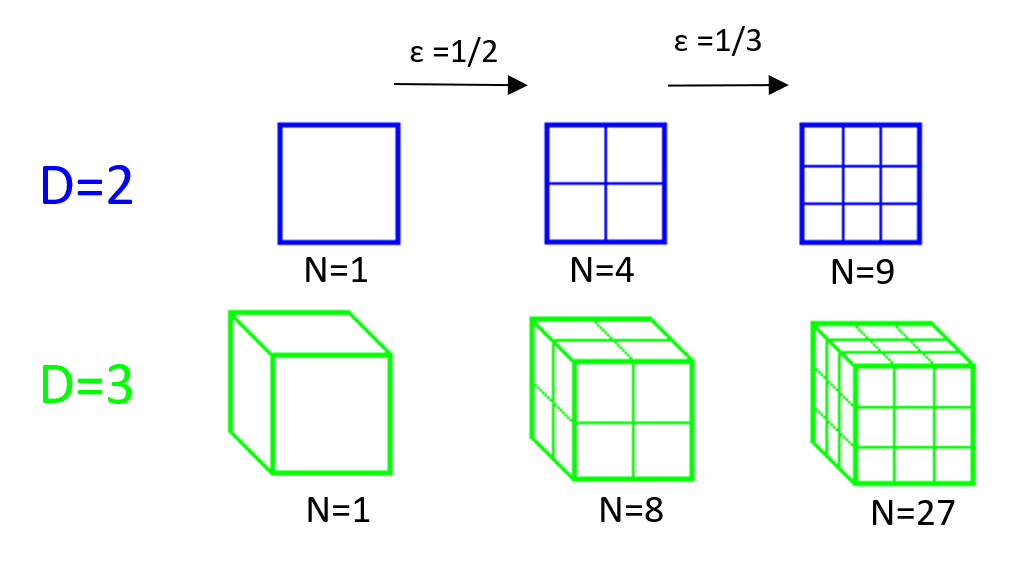
Maintenant, on cherche à trouver la dimension d’une figure fractale simple. La formule précédente nous donne :

\[D = -\frac{\log N}{\log \varepsilon}\]

Si on s’intéresse à une figure telle que la courbe de Von Koch qui consiste, à partir d’un segment, construire récursivement des triangles équilatéraux sur chaque sous-segment (cf animation ci-dessous). En comptant les segments à chaque nouvelle mise à l’échelle, on comprends que la longueur de la courbe de Koch est multipliée par $4$ pour chaque mise à l’échelle $\varepsilon=\frac{1}{3}$ (on divise les segments par 3). On trouve donc que sa dimension est $D = \frac{\log 4}{\log 3} \approx 1.26$. Il ne s’agit pas d’une simple courbe unidimensionelle, ni d’une surface mais quelque chose “entre les deux”.

Note: L’approche présentée précédemment est conceptuelle. Une définition rigoureuse et définie pour tout ensemble est la dimension de Hausdorff. Elle est peu aisée à mettre en oeuvre…

On peut différencier 3 catégories principales de fractale :

• les systèmes de fonctions itérées. Ils ont une règle géométrique fixe comme le flocon de Von Koch, le tapis de Sierpinski, la courbe de Peano.
• les fractales aléatoires. Elles sont générées par un processus stochastiques comme dans la nature ou les paysages fractales.
• les ensembles définies par une relation de récurrence en chaque point d’un espace. On peut citer l’ensemble de Julia, de mandelbrot, de lyapunov. On les appelle parfois en anglais des Escape-time fractals.

Ensemble de Julia

L’ensemble de Julia associé à un nombre complexe $c$ fixé est l’ensemble des valeurs initiales $z_0$ pour lesquelles la suite suivante est bornée :

\[\left\{ \begin{array}{ll} z_0 \in \mathbb{C} \\ z_{n+1} = z_n^2 + c \end{array} \right.\]

Pour générer un ensemble de Julia informatiquement, l’idée est de discrétiser l’espace dans un intervalle fixé pour avoir un nombre fini de valeur $z_0$ pour lesquelle on va tester la convergence de la suite.

# INITIALIZATION
# value of c fixed
c_reel, c_imag = 0.3, 0.5 
# interval limit
x_min, x_max = -1, 1
y_min, y_max = -1, 1
# discretization
size = 5000 
x_step = (x_max - x_min)/size
y_step = (y_max - y_min)/size
M = np.zeros((size,size))

Pour pouvoir travailler avec des nombres complexes, j’ai choisi de décomposer la partie réelle z_reel et la partie imaginaire z_image. Ensuite, on teste la convergence pour un point donné en regardant si on a pas dépassé un nombre fini d’itération n_iter < itermax. On peut également, en plus, vérifier que la suite $(z_n)$ est divergente si son module est strictement supérieur à $2$, z_reel**2 + z_imag**2 < 4 (cf demonstration). Finalement, on peut remplir une matrice M de $0$ ou de $1$ selon le test de convergence. Mais, pour un rendu visuelle final plus estéthique on peut également remplir la matrice M selon le taux de convergence estimé avec n_iter/itermax.

# LOOP ON ALL PIXEL = COMPLEX PLANE
for i in (range(size)):
    for j in range(size):
        n_iter = 0
        # convert pixel position to a complex number
        z_reel = i * x_step + x_min
        z_imag = j * y_step + y_min
        # update sequence until convergence
        while (z_reel**2 + z_imag**2 < 4) and (n_iter < itermax):
            z_reel, z_imag = z_reel**2 - z_imag**2 + c_reel, 2*z_imag*z_reel + c_imag
            n_iter = n_iter + 1
        # color image according to convergence rate
        M[j,i] = 255*n_iter/itermax

Astuce: En python, on aurait pu directement utiliser la fonction complex() pour avoir un objet complexe. Dans ce cas, les variables z_reel et z_imag seraient inutiles et on pourrait directement récupérer la valeur absolue et mettre au carré une unique variable complexe z.

Finalement, on peut générer des ensembles de Julia pour différentes valeurs de $c$ fixées et pour changer le visuel on peut s’amuser à tester différentes colormap. Ci-dessous quelques résultats que j’ai généré.

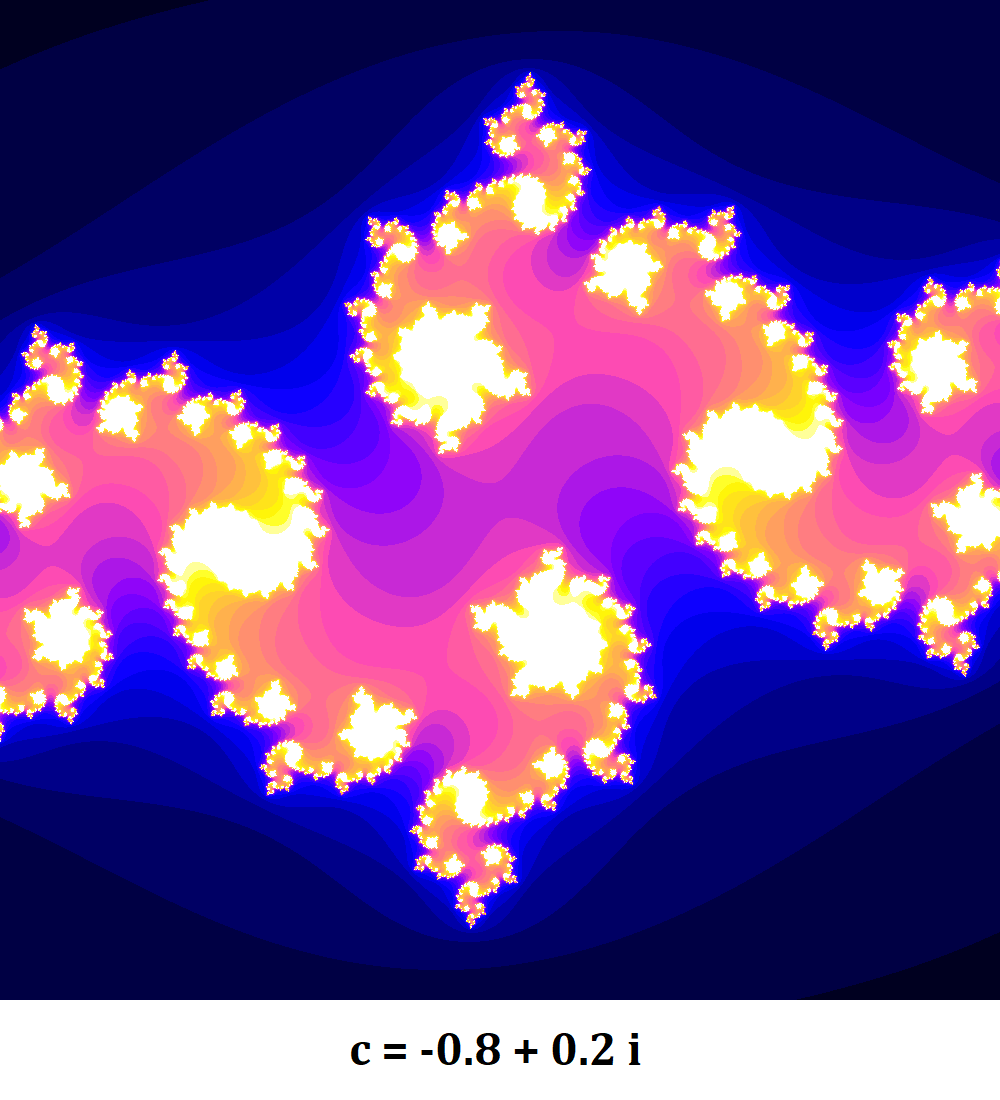
On remarque que les figures obtenues varient grandement en fonction de la valeur du complexe $c$ choisie. En fait, on peut générer les ensembles de julia pour une suite de complexes consécutifs pour voir comment les figures évoluent et en faire une animation.

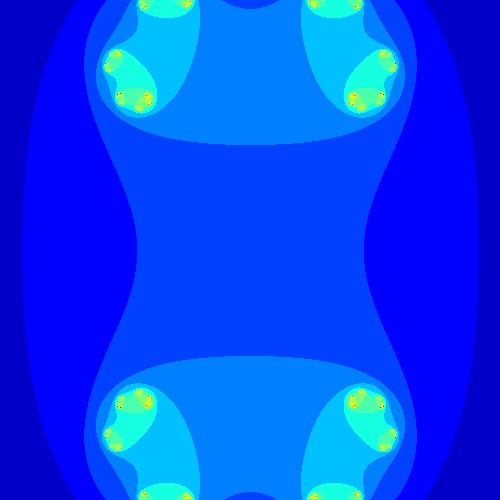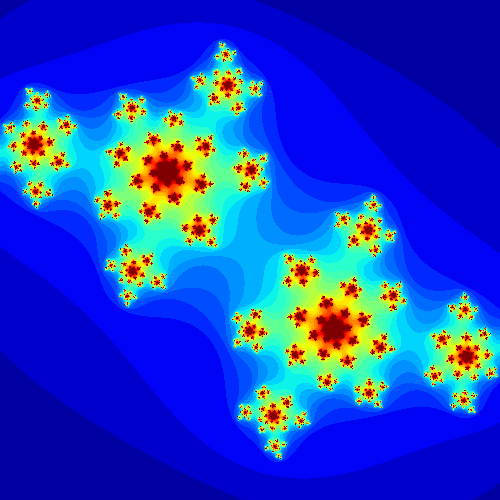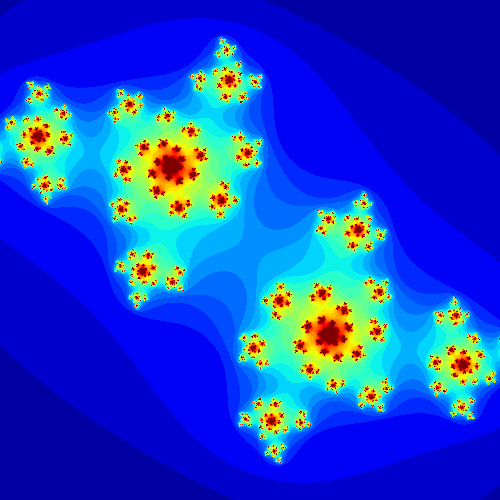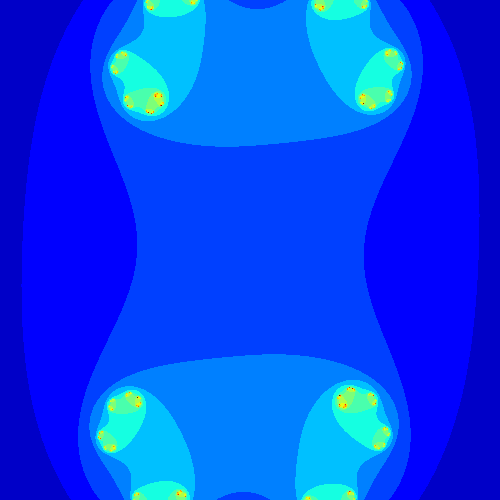
Ensemble de Mandelbrot

L’ensemble de Mandelbrot est fortement lié aux ensembles de Julia, en effet on peut définir l’ensemble de Mandelbrot $M$ comme l’ensemble des complexes $c$ pour lesquels l’ensemble de Julia $J_c$ correspondant est connexe, c’est-à-dire qu’il est fait d’un seul morceau. On peut dire que l’ensemble de Mandelbrot représente une carte des ensembles de Julia. Et, contrairement au nom qu’il porte, c’est les mathématiciens Julia et Fatou qui l’ont découvert et qui ont montré que la définition précédente est équivalente à l’ensemble des points $c$ du plan complexe $\mathbb{C}$ pour lesquels la suite suivante est bornée :

\[\left\{ \begin{array}{ll} z_0 = 0 \\ z_{n+1} = z_n^2 + c \end{array} \right.\]

Cette définition est très similaire à celle de l’ensemble de Julia à la différence qu’on s’intéresse à la variable $c$. Dans le code précédent, il faudrait modifier la ligne z_reel = i * x_step + x_min par c_reel = i * x_step + x_min et fixé z_reel = 0 (idem pour la partie imaginaire). On obtient la figure suivante :

Note: Benoît Mandelbrot est le fondateur de la théorie fractale avec notamment son article “How Long Is the Coast of Britain ? Statistical Self-Similarity and Fractional Dimension” en 1967. C’est également lui qui obtient pour la première fois, une visualisation par ordinateur de cet ensemble.

Logiciels

La génération de fractale n’est pas une tâche facile : beaucoup de paramètres peuvent être à prendre en compte et les temps de calcul sont souvent long. Dans les figures que j’ai généré, on ne voit pas au premiers abords le caractère auto-similaire des fractales, il faudrait changer d’échelle en zoomant de plus en plus profond sur un point du plan.

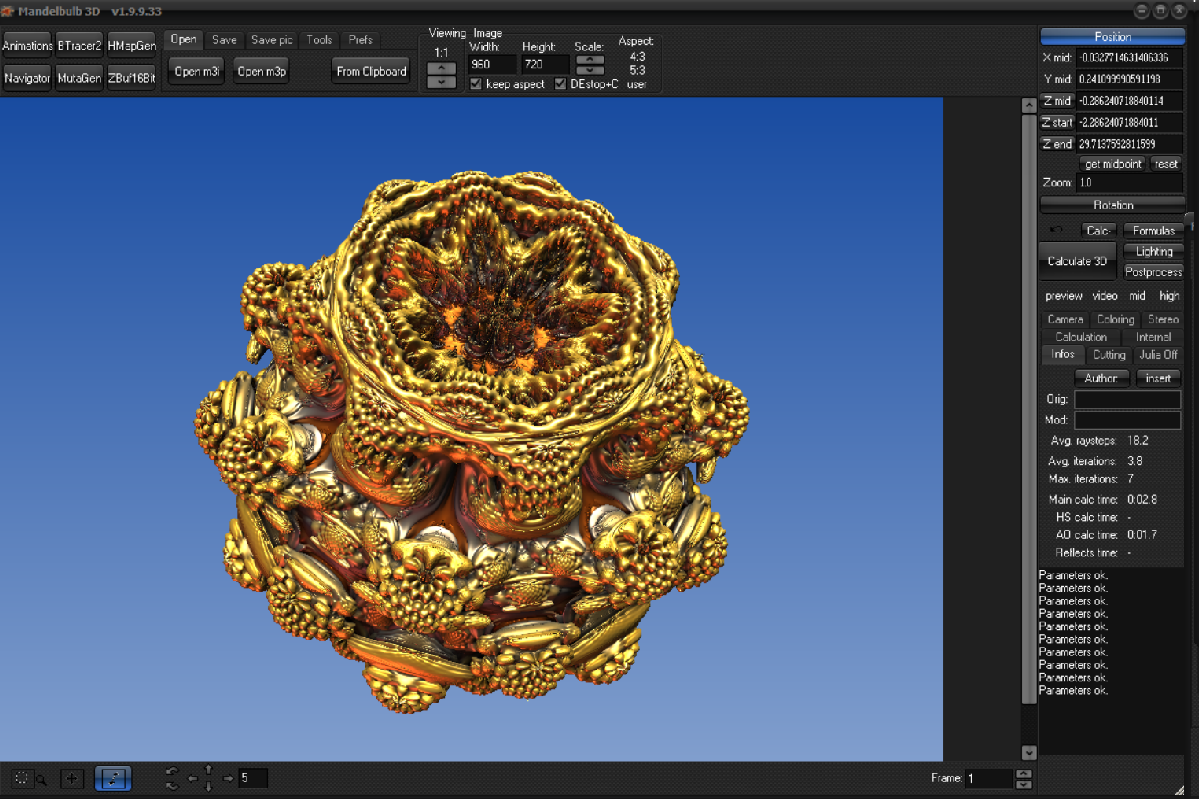
Il existe de nombreux logiciels générateur de fractal gratuits disponibles. Ils sont souvent optimisés pour faire du multi-processing ou du calcul sur GPU, possèdent une interface graphique pour gérer les nombreux paramètres et sont parfois capables de créer des objets 3D (comme les 3 affichés ci-dessous). Une liste assez complète est disponible ici.

Mandelbul3D	Mandelbuler	Fragmentarium

Et pour ceux qui ne veulent pas se compliquer et juste se laisser porter par la géométrie psychédélique des fractales sans effort, vous pourrez trouver sur internet des gens qui ont déjà fait le travail à votre place. On trouve sur youtube une floppée de vidéos comme par exemple The Hardest Trip - Mandelbrot Fractal Zoom qui zoome pendant 2h30 sur un point précis du plan complexe.

---