Dynamique des populations : EDO, écologie, logistique

10 minute(s) de lecture

Parmis les enjeux du 21^ème siècle, l’écologie a un rôle majeure puisqu’elle est la science qui étudie les interactions des êtres vivants entre eux et avec leur milieu. Pour modéliser ces interactions, la dynamique des populations est la branche qui s’intéresse aux fluctuations démographiques des espèces. Ses applications sont nombreuses puisqu’elle peut permettre de répondre à des problèmes variés comme la gestion d’espèces menacées, la protection des cultures contre des nuisibles, le contrôle de bioréacteurs ou la prédiction des épidémies.

Modèle de Verhulst

À la fin du 18^ème siècle, le modèle de Malthus décrit la variation d’une taille de population $y$ au cours du temps $t$ par l’équation différentielle ordinaire¹ (EDO) :

\[y'(t) = (n-m) y(t) = r y(t)\]

avec les constantes : $n$ le taux de natalité, $m$ le taux de mortalité et $r$ le taux de croissance. Ce modèle nous dit que, selon le taux de croissance $r$, la taille des populations peut soit diminuer, rester constante ou augmenter de manière exponentielle. Ce modèle ne reflète pas la réalité puisque une population n’augmentera jamais à l’infini.

En 1840, Verlhust propose un modèle de croissance plus adapté en partant de l’hypothèse que le taux de croissance $r$ n’est pas une constante mais est fonction affine de la taille de population $y$ :

\[y'(t) = \big(n(y) - m(y)\big) y(t)\]

Verlhust part notamment de l’hypothèse que plus la taille d’une population augmente alors plus son taux de natalité $n$ diminue et plus son taux de mortalité $m$ augmente. En partant de cette hypothèse et en appliquant quelques manipulations algébriques astucieuses, on peut montrer que l’équation différentielle précédente peut se réécrire sous la forme :

\[y'(t) = r y(t) \left(1 - \frac{y(t)}{K}\right)\]

avec $K$ une constante appelée capacité d’accueil. On peut résoudre analytiquement cette équation avec la condition initiale $y(t=0)=y_0$, on obtient la solution logistique :

\[y(t) = \frac{K}{1+\left(\frac{K}{y_0}-1\right)e^{-rt}}\]

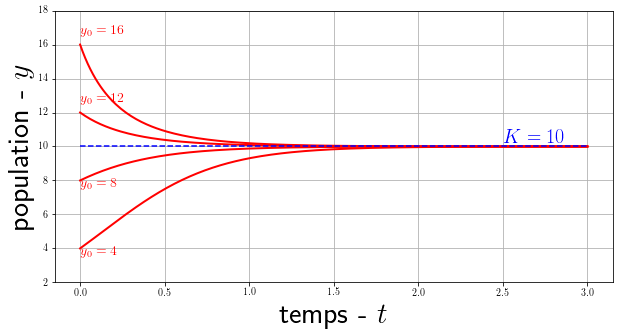
Résolution détaillée de l'équation différentielle logistique par séparation de variable

$$ \begin{align*} \int_{y_0}^{y(t)} \frac{1}{y(1-y/K)}dy &= \int_0^t r \ d\tau \\ \int_{y_0}^{y(t)} \frac{K}{y(K-y)}dy &= \int_0^t r \ d\tau \\ \int_{y_0}^{y(t)} \frac{1}{y}dy + \int_{y_0}^{y(t)} \frac{1}{K-1}dy &= \int_0^t r \ d\tau \\ \ln \left| \frac{y(t)}{y_0} \right| - \ln \left| \frac{K-y(t)}{K-y_0} \right| &= r \ t \\ \ln \left( \frac{y(t)\big(K-y_0\big)}{y_0\big(K-y(t)\big)} \right) &= r \ t \\ \frac{y(t)}{K-y(t)} &= \frac{y_0}{K-y_0}e^{rt} \\ y(t)\left(1+\frac{y_0}{K-y_0}e^{rt} \right) &= \frac{K y_0 e^{rt}}{K-y_0} \\ y(t) &= \frac{Ky_0e^{rt}}{K-y_0+y_0e^{rt}} \\ y(t) &= \frac{K y_0}{(K-y_0)e^{-rt}+y_0} \\ \end{align*} \\ \square $$

On remarque que $ \lim\limits_{t\to\infty} y(t) = K $. Ce qui signifie que peut importe la taille de la population initiale $y_0$, la population finira toujours par tendre vers $K$ la capacité d’accueil qu’on qualifie souvent comme le nombre d’individus maximal que le milieu peut accueillir (selon l’espace, les ressources …). Cette fonction dite logistique introduite pour la première fois par Verlhust pour modéliser la croissance des populations trouvera par la suite plein d’application dans des domaines variés comme l’économie, la chimie, les statistiques et plus récemment les réseaux de neurones artificielles.

Modèle de Lotka-Volterra

Les modèles de Lotka-Volterra sont des sytèmes d’équations simples qui sont apparus au début du 20^ème siècle. Ils portent le nom de deux mathématiciens qui ont publié en même temps mais indépendamment sur le sujet : Volterra, en 1926, pour modéliser les populations de sardines et de leurs prédateurs et Lotka, en 1924, dans son livre Elements of Physical Biology. Contrairement au modèle de Verlhust qui s’intéresse à une seule population, les modèles de Lotka-Volterra modélisent les interactions entre plusieurs espèces, chacune ayant un impact sur le développement de l’autres.

Proie-prédateur

Le modèle proie-prédateur de Lotka-Volterra a permis d’expliquer des données collectées de certaines populations d’animaux comme le lynx et lièvre ainsi que le loup et l’élan aux Etats-Unis. On y représente l’évolution du nombre proies $x$ et de prédateurs $y$ au cours du temps $t$ selon le modèle suivant :

\[\left\{ \begin{array}{ccc} x'(t) = x(t)\ \big(\alpha - \beta y(t)\big) \\ y'(t) = y(t)\ \big( \delta x(t) - \gamma\big) \end{array} \right.\]

avec les paramètres $\alpha$ et $\delta$ sont les taux de reproduction respectivement des proies et des prédateurs et $\beta$ et $\gamma$ sont les taux de mortalité, respectivement, des proies et des prédateurs.

Note: On parle de système autonome : le temps $t$ n’apparaît pas explicitement dans les équations.

Si on développe chacune des équations, on peut plus facilement donner une interprétation. Pour les proies, on a d’une part le terme $\alpha x(t)$ qui modélise la croissance exponentielle avec une source illimitée de nourriture et d’autre part $- \beta x(t) y(t)$ qui représente la prédation proportionnelle à la fréquence de rencontre entre prédateurs et proies. L’équation des prédateurs est très semblable à celle des proies, $\delta x(t)y(t)$ est la croissance des prédateurs proportionnelle à la quantité de nourriture disponible (les proies) et $- \gamma y(t)$ représente la mort naturelle des prédateurs.

On peut caculer les équilibres de ce système d’équations différentielles et également en déduire un comportement mais les solutions n’ont pas d’expression analytique simple. Néanmoins, il est possible de calculer une solution approchée numériquement (plus de détails dans la section suivante).

# define ODE function to resolve
r, c, m, b = 3, 4, 1, 2
def prey_predator(XY, t=0):
    dX = r*XY[0] - c*XY[0]*XY[1]
    dY = b*XY[0]*XY[1] - m*XY[1]
    return [dX, dY]

# discretization
T0   = 0
Tmax = 12
n    = 200
T    = np.linspace(T0, Tmax, n) 

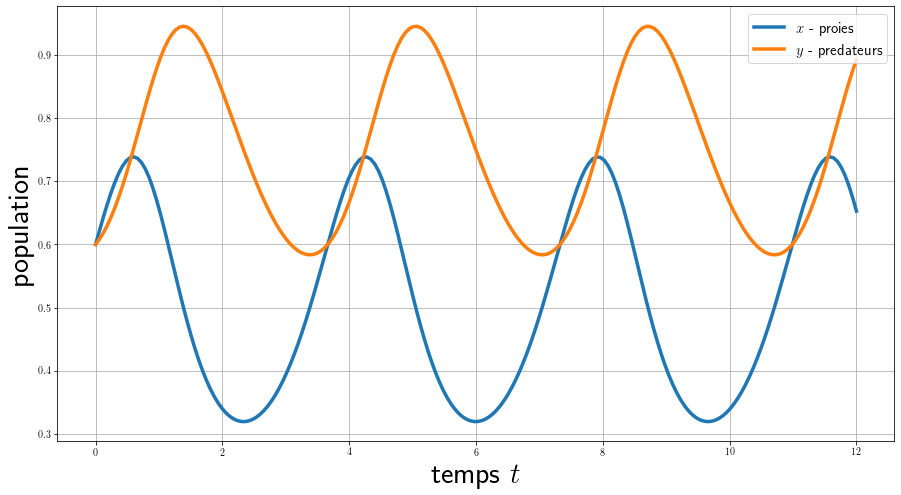
On calcule ici l’évolution des 2 populations en fonction du temps pour une condition initiale fixée, on voit qu’elles ont un comportement périodique et en décalage de phase.

# TEMPORAL DYNAMIC
X0 = [1,1]
solution = integrate.odeint(prey_predator, X0, T) # use scipy solver

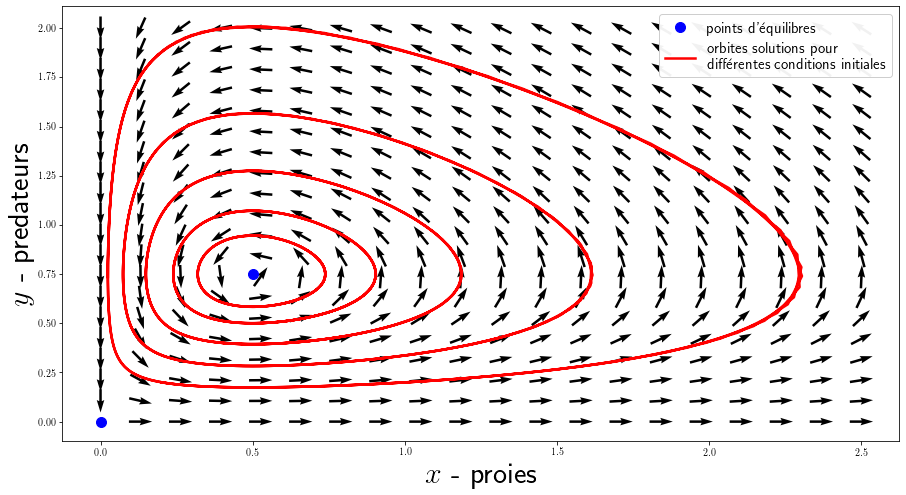
Ici, on calcule plusieurs solutions pour différentes conditions initiales qu’on affiche dans l’espace de phase (le temps n’appararaît pas). On peut également afficher le champ de vecteur généré par le système d’équation avec plt.quiver() pour une grille de valeur.

# PHASES SPACE
# some trajectories
orbits = []
for i in range(5):
    X0    = [0.2+i*0.1, 0.2+i*0.1]
    orbit = integrate.odeint(prey_predator, X0, T)
    orbits.append(orbit) 
# vector field
x, y             = np.linspace(0, 2.5, 20), np.linspace(0, 2, 20)
X_grid, Y_grid   = np.meshgrid(x, y)                      
DX_grid, DY_grid = prey_predator([X_grid, Y_grid])
N                = np.sqrt(DX_grid ** 2 + DY_grid ** 2) 
N[N==0]          = 1
DX_grid, DY_grid = DX_grid/N, DY_grid/N

Attention: Les unités des simulations ne reflète pas la réalité, il faut des populations suffisamment grandes pour que la modélisation soit correcte.

Dans le modèle utilisé, les prédateurs prospèrent lorsque les proies sont nombreuses, mais finissent par épuiser leurs ressources et déclinent. Lorsque la population de prédateurs a suffisamment diminué, les proies profitant du répit se reproduisent et leur population augmente de nouveau. Cette dynamique se poursuit en un cycle de croissance et déclin. Il existe 2 équilibres : le point $(0,0)$ est un point de selle instable qui montre que l’extinction des 2 espèce est en fait quasiment impossible à obtenir et le point $(\frac{\gamma}{\delta}, \frac{\alpha}{\beta})$ est un centre stable, les populations oscillent autour cet état.

Note: Cette modélisation reste assez simple, un grande nombre de variante existe. On peut rajouter des termes de disparition des 2 espèces (dus à la pêche, chasse, pesticide …), tenir compte de la capacité d’accueil du milieu en utilisant un terme logistique.

Compétition

Le modèle de compétition de Lotka-Volterra est une variante du modèle de prédation où les 2 espèces n’ont pas une hierarchie de proies et prédateurs mais sont en compétition l’une et l’autre. De plus, la dynamique de base n’est plus une simple croissance exponentielle mais logistique (avec les paramètres $r_i$ et $K_i$) :

\[\left\{ \begin{array}{ccc} x_1'(t) = r_1x_1(t)\left(1- \frac{x_1(t)+\alpha_{12}x_2(t)}{K_1}\right) \\ x_2'(t) = r_2x_2(t)\left(1- \frac{x_2(t)+\alpha_{21}x_1(t)}{K_2}\right) \end{array} \right.\]

avec $\alpha_{12}$ l’effet de l’espèce 2 sur la population de l’espèce 1 et réciproquement $\alpha_{21}$ l’effet de l’espèce 2 sur l’espèce 1. Par exemple, pour l’équation de l’espèce 1, le coefficient $\alpha_{12}$ est multiplié par la taille de la population $x_2$. Quand $\alpha_{12} < 1$ alors l’effet de l’espèce 2 sur l’espèce 1 est plus petit que l’effet de l’espèce 1 sur ces propres membres. Et inversement, quand $\alpha_{12} > 1$, l’effet de l’espèce 2 sur l’espèce 1 est supérieur à l’effet de l’espèce 1 sur ces propres membres.

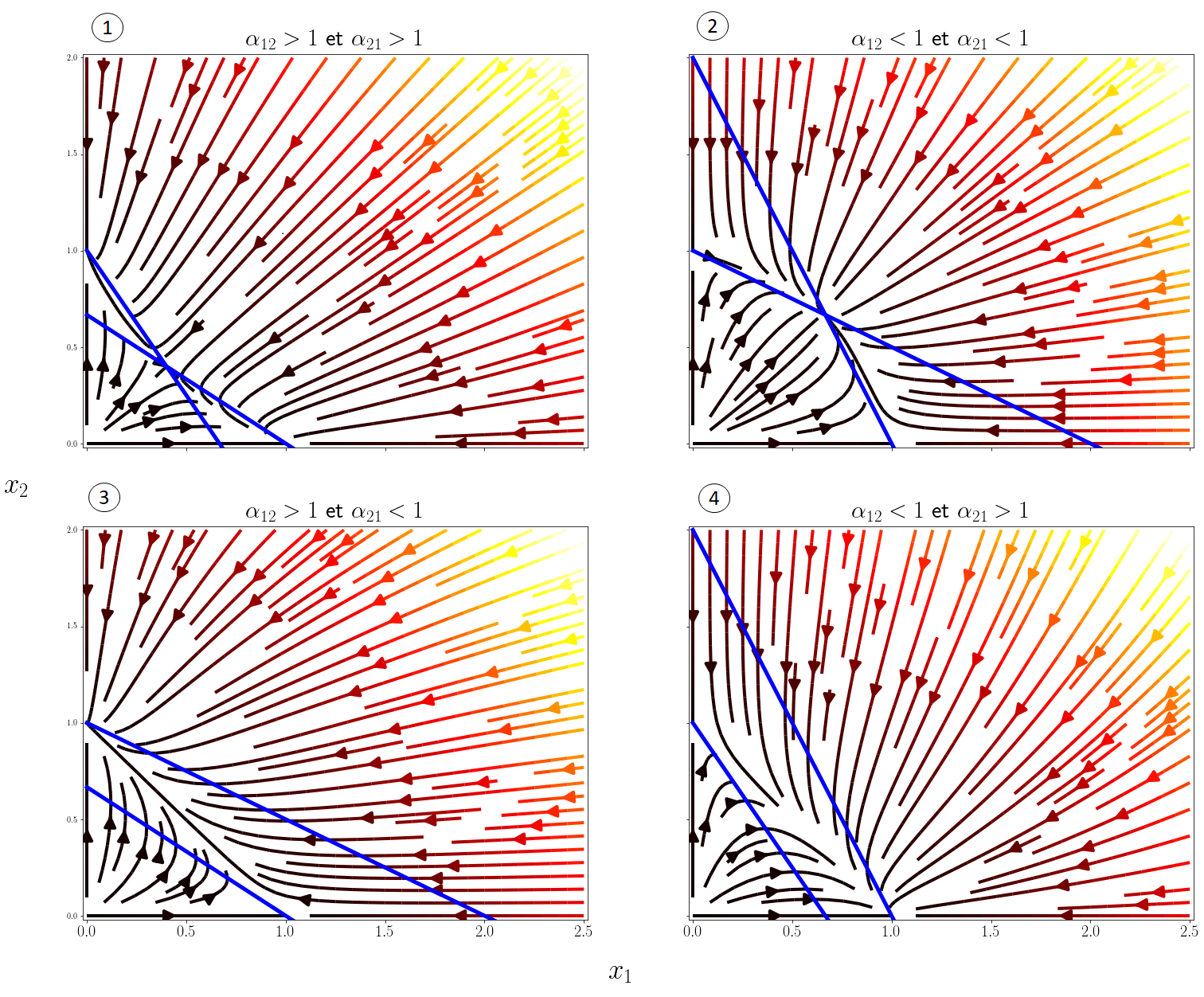
Pour comprendre plus en détails les prédictions du modèles, il est utile de tracer comme précédemment les diagrammes d’espace de phase $(x_1,x_2)$. On peut distinguer 4 scénarios selon les valeurs des coefficients de compétition, j’affiche ci-dessous les champs de vecteurs de ces scénarios avec plt.streamplot() ainsi que les isoclines, les courbes pour lesquelles $x_1'(t)=0$ ou $x_2'(t)=0$:

# define ODE to resolve
r1, K1 = 3, 1
r2, K2 = 3, 1
def competition(X1X2, a1, a2):
    dX1 = r1*X1X2[0] * (1-(X1X2[0]+a1*X1X2[1])/K1)
    dX2 = r2*X1X2[1] * (1-(X1X2[1]+a2*X1X2[0])/K2)
    return [dX1, dX2]

# compute derivatives for each scenario
N = 20
x, y = np.linspace(0, 2.5, N), np.linspace(0, 2, N)
X_grid, Y_grid = np.meshgrid(x, y)
DX_grid, DY_grid = np.zeros((4,N,N)), np.zeros((4,N,N))
coeffs = np.array([[1.5,1.5],[0.5,0.5],[1.5,0.5],[0.5,1.5]])
for k,(a1,a2) in enumerate(coeffs):
    DX_grid[k,:], DY_grid[k,:] = competition([X_grid, Y_grid], a1, a2)

Au final, les 4 comportements possibles en fonction de $\alpha_{12}$ et $\alpha_{21}$ sont les suivants :

Exclusion compétitive d’une des deux espèces en fonction des conditions initiales.
Coexistence stable des deux espèces.
Exclusion compétitive de l’espèce 1 par l’espèce 2.
Exclusion compétitive de l’espèce 2 par l’espèce 1.

La coexistence stable des 2 espèces n’est possible que si $\alpha_{12} < 1$ et $\alpha_{21} < 1$, c’est-à-dire qu’il faut que la compétition interspécifique soit plus faible que la compétition intraspécifique.

Méthode numérique pour les EDO

Cette section est un petit peu à part du réel sujet de ce post puisque j’y introduis les méthodes numériques pour résoudre les équations différentielles. En effet, il est possible de déduire de nombreuses propriétés d’un système d’EDO en se basant sur les théorèmes mathématiques pour la théorie des systèmes dynamiques (méthode de Lyapunov, invariance de LaSalle, théorème de Poincaré-Bendixon …) mais seul un nombre restreint d’équations différentielles admettent une solution analytique. En pratique, on préfère souvent avoir une méthode qui calcule une solution approximative du problème à tout temps $t$. On considère le problème $y'(t) = f\big(t,y(t)\big)$ avec $y(t_0)=y_0$. L’idée des méthodes numériques est de résoudre le problème sur un ensemble discret de points $(t_n,y_n)$ avec $h_n=t_{n+1}-t_n$, un pas de temps fixé.

Euler

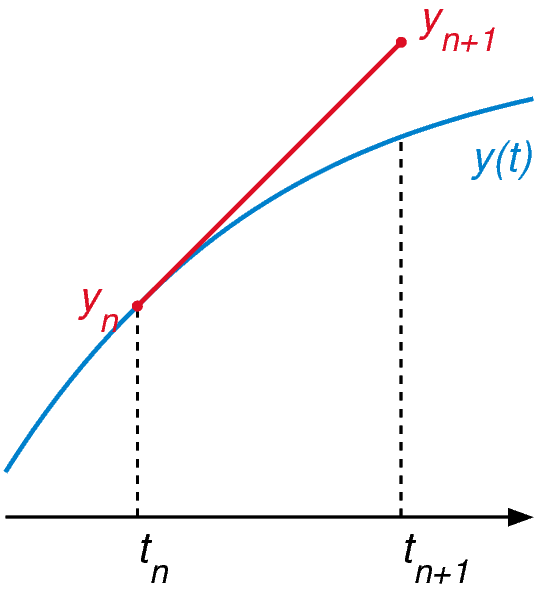image-right La méthode d’Euler est la plus basique des méthodes numériques pour EDO, elle utilise l’équation différentielle pour calculer la pente de la tangente à n’importe quel point de la courbe solution. La solution est approchée en partant du point initial $y_0$ connu pour lequel on calcule la tangente, on fait ensuite un pas de temps le long de cette tangente on obtient alors un nouveau point $y_1$. L’idée est de répéter ce processus, pour un pas de temps de $t_n$ à $t_{n+1}$ on peut l’écrire comme $y_{n+1} = y_n + h f(t_n,y_n)$.

Cette méthode est très simple à mettre en place, par exemple en python :

def Euler_method(f, y0, t):
    y = np.zeros((len(t), len(y0)))
    y[0,:] = y0
    for i in range(len(t)-1):
        y[i+1] = y[i] + h*f(y[i], t[i])
    return y

Runge-Kutta

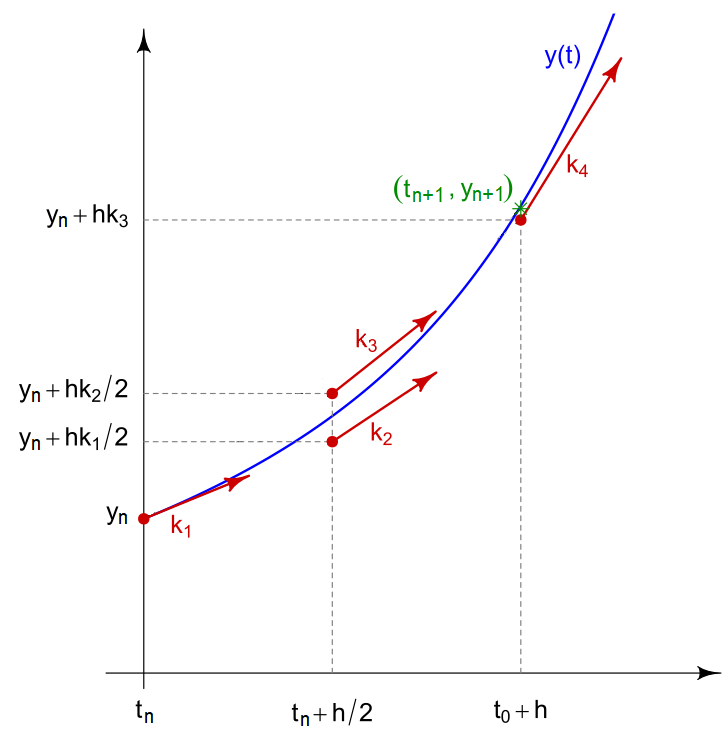image-right Les méthodes de Runge-Kutta sont une famille de méthodes, la plus connue est celle d’ordre 4. Elle est plus précise que la méthode d’Euler en faisant une moyenne pondérée de 4 termes correspondant à différentes pentes de la courbe dans l’intervalle de temps fixé. On la définit par :

\[y_{n+1} = y_n + \frac{h}{6} (k_1+2k_2+2k_3+k_4)\]

avec :

$k_1=f(t_n,y_n)$
$k_2=f(t_n+h/2,y_n+hk_1/2)$
$k_3=f(t_n+h/2,y_n+hk_2/2)$
$k_4=f(t_n,y_n+hk_3)$

def RungeKutta4_method(f, y0, t):
    y = np.zeros((len(t), len(y0)))
    y[0] = y0
    for i in range(len(t)-1):
        k1 = f(y[i], t[i])
        k2 = f(y[i]+k1*h/2, t[i]+h/2)
        k3 = f(y[i]+k2*h/2, t[i]+h/2)
        k4 = f(y[i]+k3*h, t[i]+h)
        y[i+1] = y[i] + (h/6) * (k1 + 2*k2 + 2*k3 + k4)
    return y

Exemple

Pour vérifier le comportement de ces méthodes, j’ai choisi de les testées sur un modèle bien connu de la physique : l’oscillateur harmonique. Dans sa forme la plus simple, on peut calculer exactement la solution du problème et donc comparer nos méthodes de résolution approchées. Le problème peut s’écrire :

\[\left\{ \begin{array}{ccc} y''(t) + y(t) = 0 \\ y(0) = y_0 \end{array} \right.\]

et admet pour solution $ y(t) = y_0 \cos(t) $.

# initial condition
y0 = [2, 0]
# discretization
t = np.linspace(0, 5*pi, 100)
h = t[1] - t[0]
# ODE formulation
def problem(y, t):
    return np.array([y[1], -y[0]])
# analytic solution
def exact_solution(t):
    return y0[0]*np.cos(t)
y_exact = exact_solution(t)
y_euler = Euler_method(problem, y0, t)[:, 0]
y_rk4   = RungeKutta4_method(problem, y0, t)[:, 0]    

Comme attendu la méthode de Runge-Kutta est bien plus précise que la méthode d’Euler (mais plus lente). L’erreur des méthodes numériques diminue en fonction de la taille du pas de temps $h$ mais plus $h$ est petit et plus le temps de calcul est long. En théorie, pour analyser les méthodes numériques on se base sur 3 critères :

la convergence qui garantit que la solution approchée est proche de la solution réelle.
l’ordre qui quantifie la qualité de l’approximation pour une itération.
la stabilité qui juge du comportement de l’erreur.

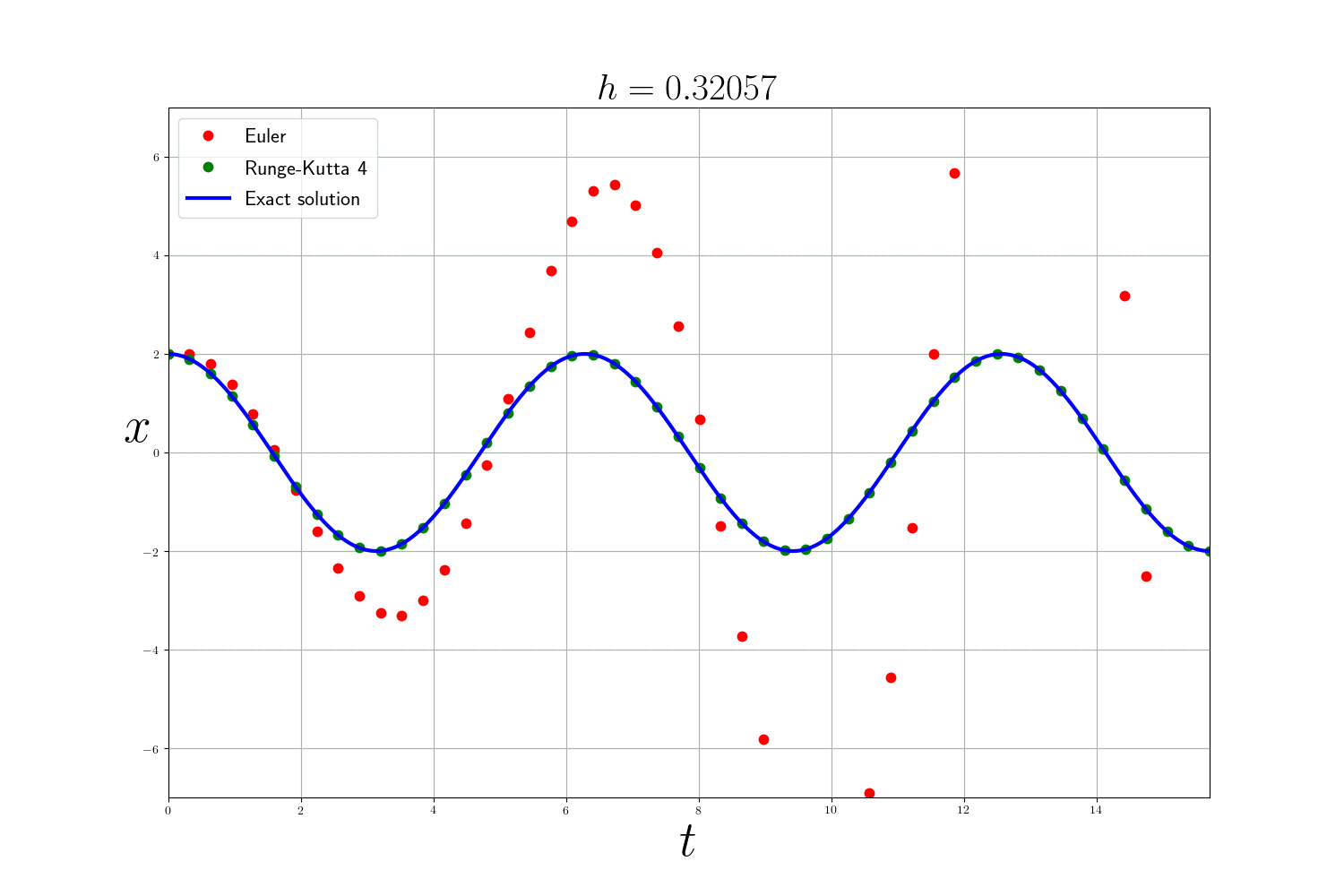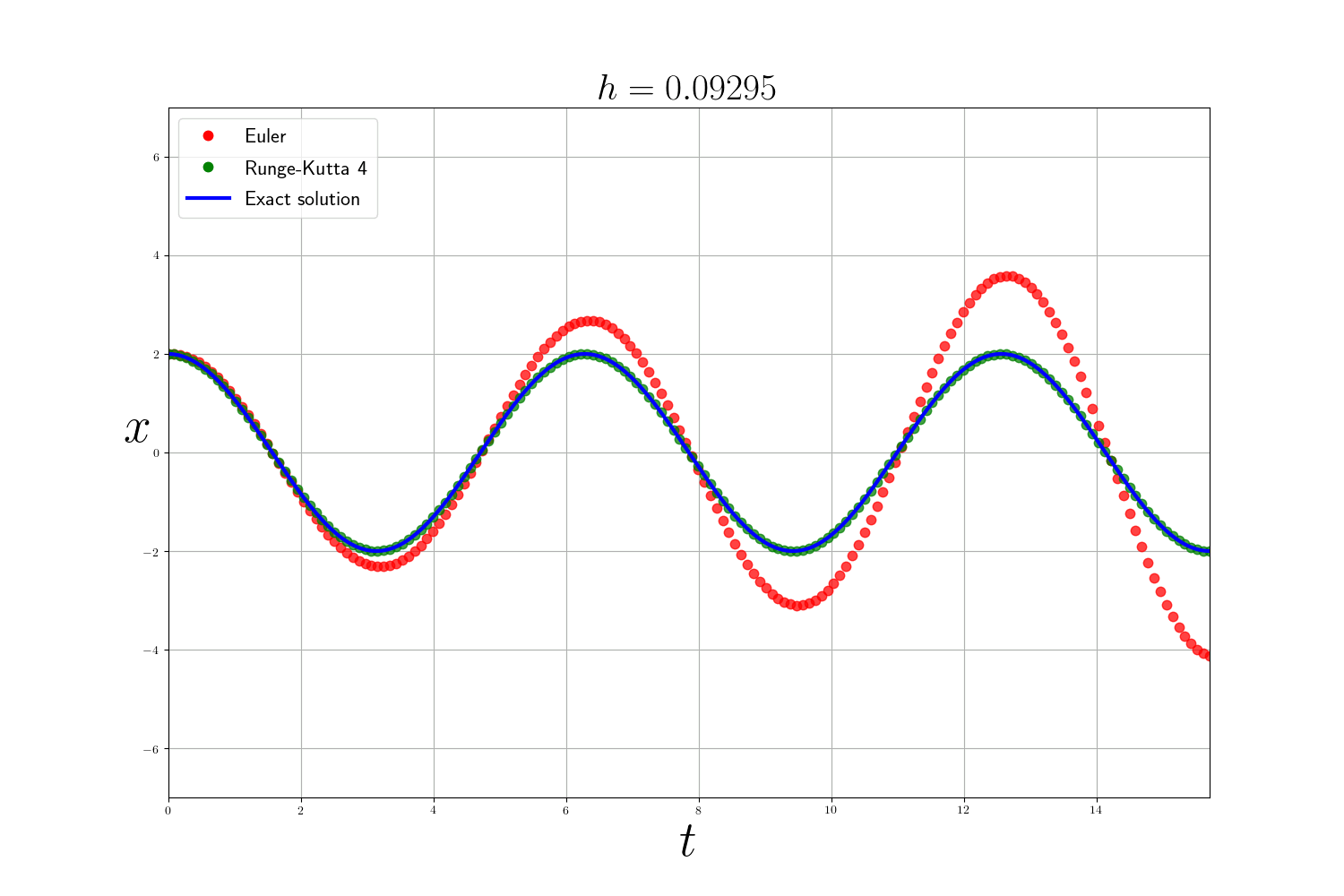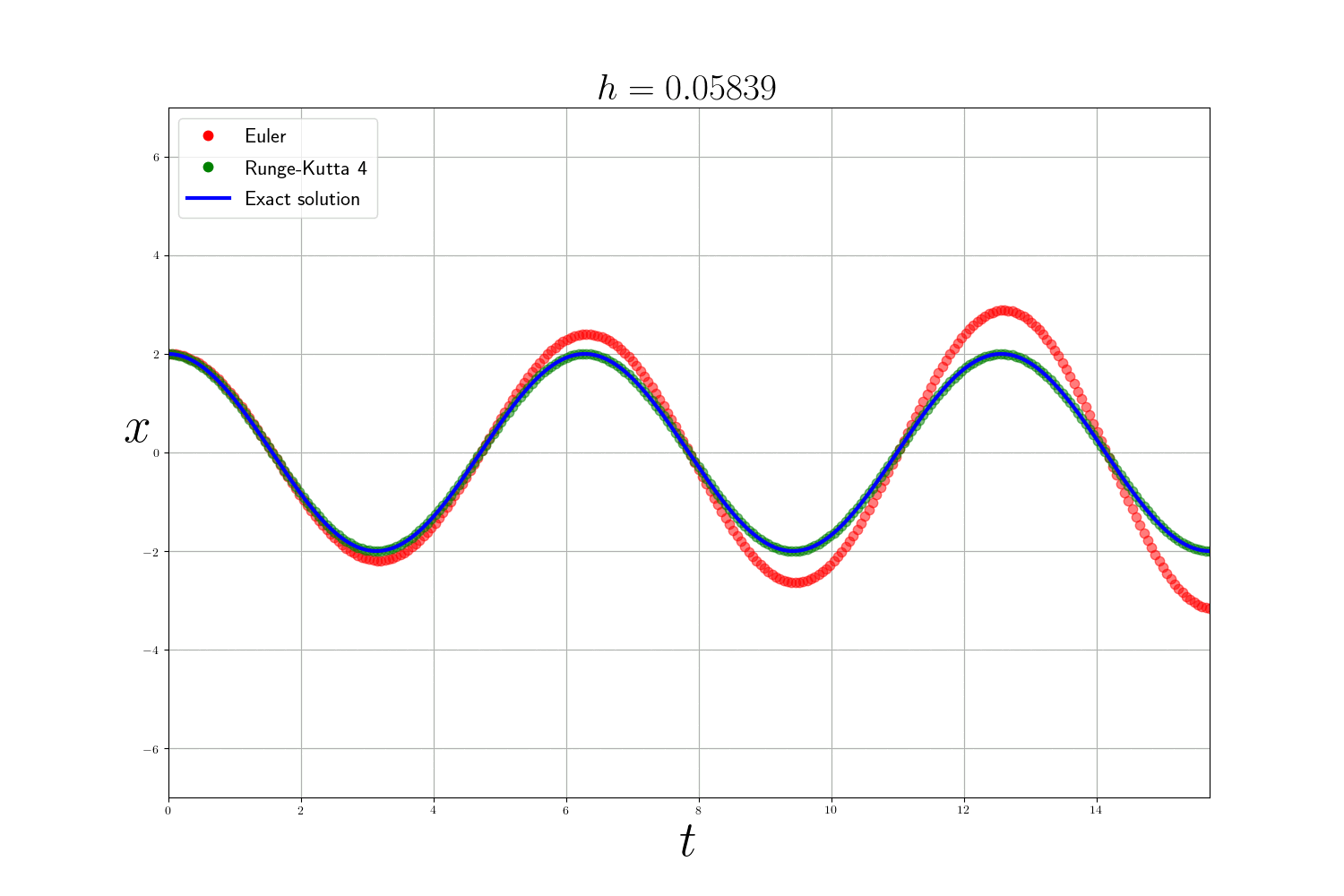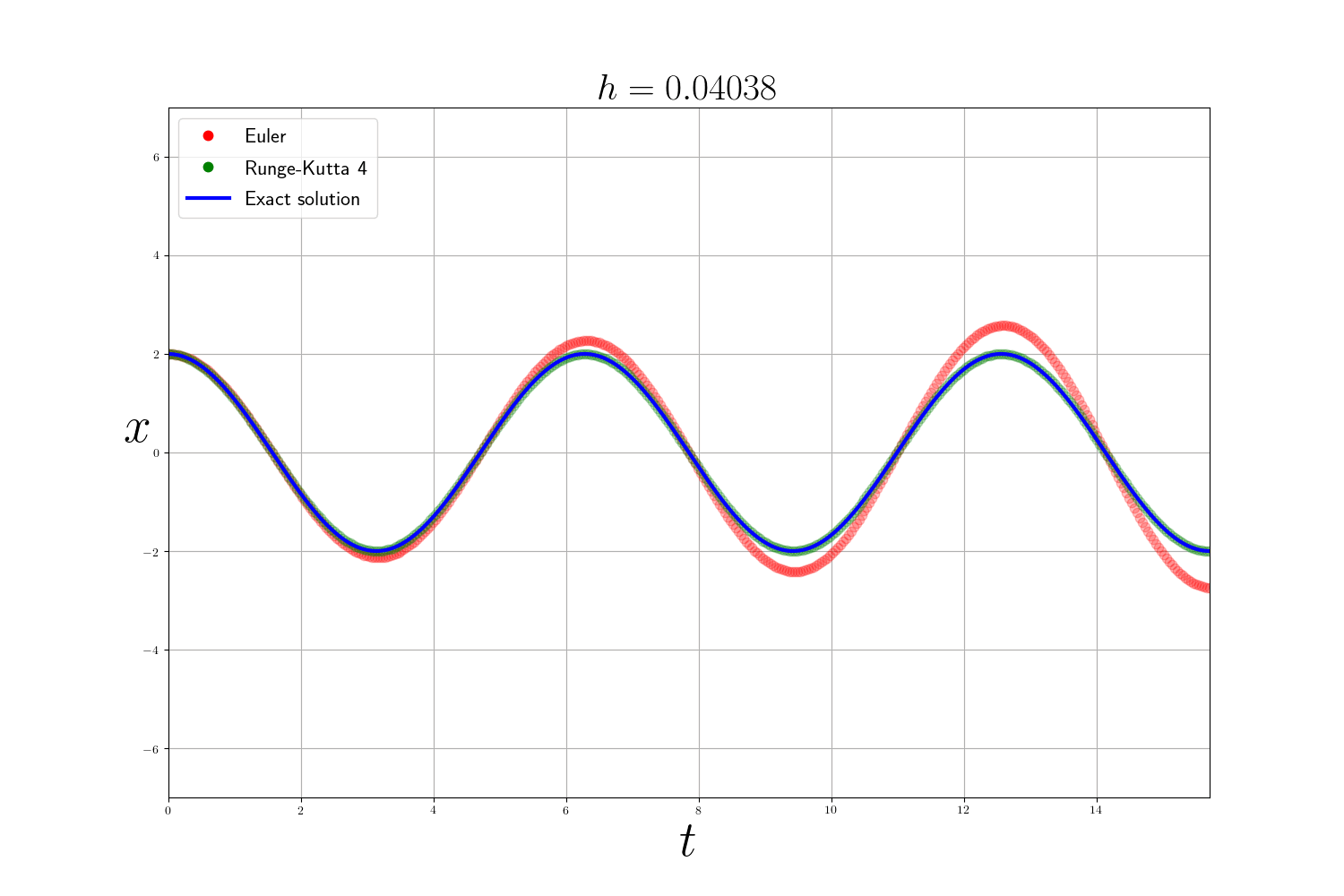
En pratique : Dans les problèmes précédents , j’utilise la fonction integrate.odeint(f, y0, t) de scipy qui est un solveur d’EDO plus avancé qui utilise la méthode d’Adams–Bashforth

Le terme ordinaire est utilisé par opposition au terme équation différentielle partielle (ou équation aux dérivées partielles) où la ou les fonctions inconnues peuvent dépendre de plusieurs variables. ↩

Julien Guégan