Optimisation : algorithme, XFOIL, profil d’aile

9 minute(s) de lecture

Dans la vie de tous les jours, on cherche souvent à optimiser nos actions pour faire le moins d’effort et bien, dans le monde de l’ingénierie, c’est la même chose. Les problèmes de minimisation sont omniprésents dans de nombreux systèmes que ce soit pour obtenir un gain de temps, d’argent, d’énergie, de matière première, ou encore de satisfaction. On peut par exemple chercher à optimiser un trajet, la forme d’un objet, un prix de vente, une réaction chimique, le contrôle aérien, le rendement d’un appareil, le fonctionnement d’un moteur … La complexité des problèmes et de leur modélisation fait de l’optimisation une branche des mathématiques très vaste et variée, en pratique la qualité des résultats dépend de la pertinence du modèle, du bon choix des variables que l’on cherche à optimiser, de l’efficacité de l’algorithme et des moyens pour le traitement numérique. Dans le domaine de l’aérodynamisme, la forme des avions et des voitures de courses est souvent designer pour que l’énergie dépensée soit minimum. Après avoir introduit quelques aspects algorithmiques du problème de minimisation, l’article suivant présentera comment le profil d’une aile d’avion peut être optimisé pour maximiser ses performances.

Algorithmes d’optimisation

Face à la résolution d’un problème d’optimisation, une 1^ère étape est d’identifier à quelle catégorie il appartient. En effet, les algorithmes sont plus ou moins adaptés pour des catégories données puisque le problème peut être continue ou discret, avec ou sans contraintes, différentiable ou non, convexe ou non … On écrit un problème d’optimisation sans contraintes simplement :

\[\min_{x \in X} f(x)\]

où $f$ peut être appelée fonction objectif ou fonction coût. En théorie, pour des problèmes non contraints, on peut trouver le(s) minimum(s) en regardant quand $ \nabla f(x) = 0 $ (condition du premier ordre) et la positivité de la hessienne $H(x)$ (condition du second ordre). Pour un problème avec contraintes, les conditions de Kuhn-Tucker appliquées à la fonction Lagrangienne permettent de transformer le problème en un nouveau sans contraintes mais avec des inconnues supplémentaires.

Note: Un problème de maximisation peut être facilement transposer en un problème de minimisation : $\max_{x \in X} f(x) \Leftrightarrow \min_{x \in X} - f(x)$

Pour des cas simples, on peut donc résoudre analytiquement le problème. Par exemple, lorsque $f$ a une forme quadratique, linéaire et sans contrainte, annuler le gradient revient à résoudre un système linéaire. Mais, en pratique, le gradient peut avoir une forme trop compliqué ou même la fonction $f$ peut ne pas avoir de forme analytique connue (elle peut être le résultat d’une d’EDP résolu numériquement par exemple). Il existe donc une grande variété d’algorithmes d’optimisation itératifs pour essayer de trouver le minimum, certains étant plus ou moins adaptés à certains type de problème. D’autre part, il est courant de valider ces algorithmes en les testant sur des fonctions connues pour lesquelles on connaît analytiquement la valeur du vraie mimimum, elles permettent d’évaluer les caractéristiques des approches comme la vitesse de convergence, la robustesses, la précision ou le comportement général. Une liste assez complète de ces fonctions test est disponible sur wikipedia.

Par soucis de simplicité, les 3 approches ci-dessous sont des approches simples qui permettent d’introduire les notions basiques des algorithmes d’optimisation, elles seront testées sur la fonction test de Himmelblau. Dans la réalité, on fait le plus souvent appelle a des librairies ou logiciels spécialisés qui implémentent des approches bien plus sophistiquées.

Descente de gradient

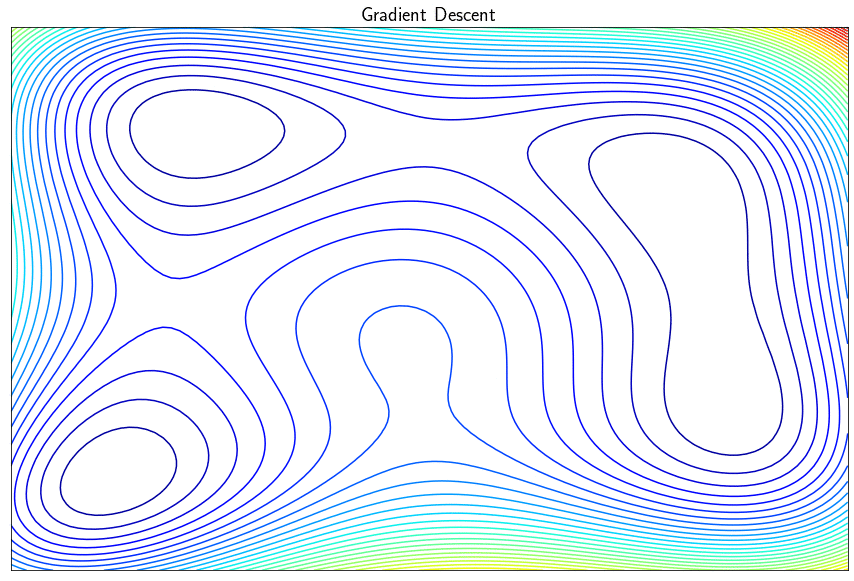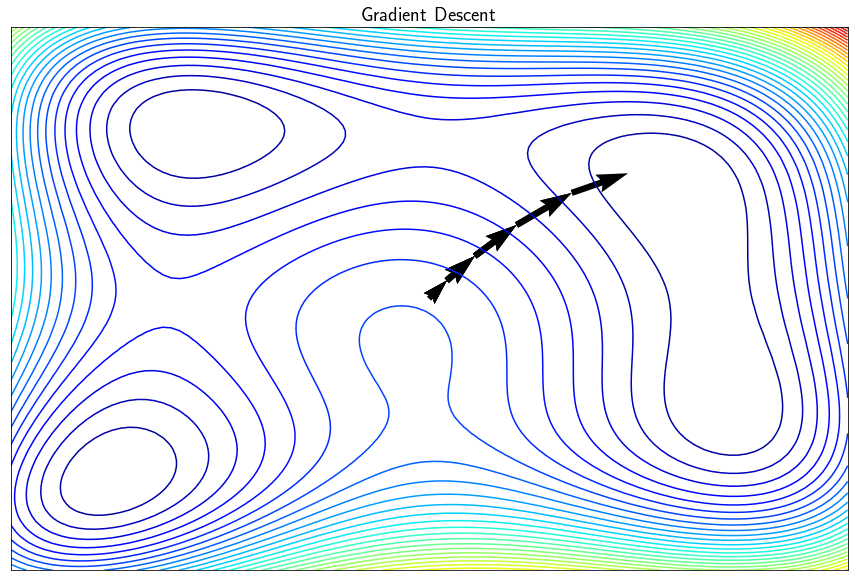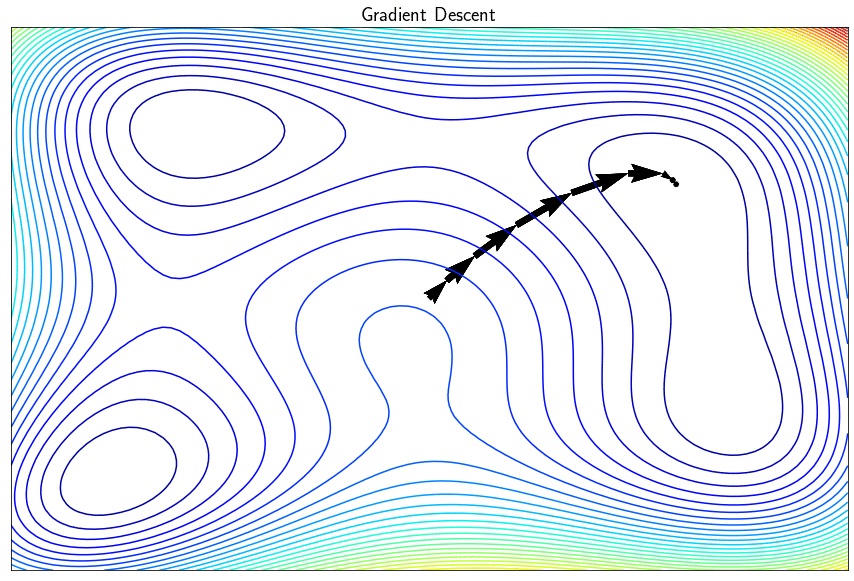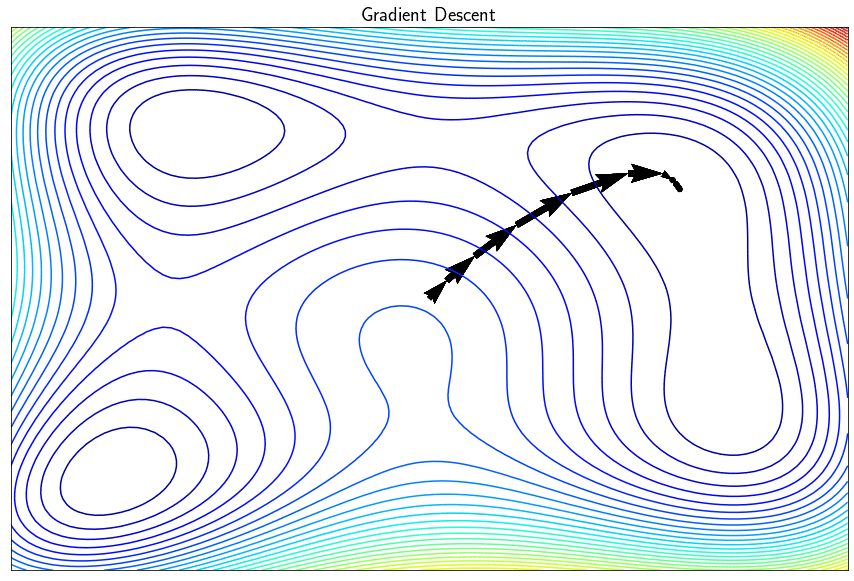image-right L’algorithme de descente de gradient permet de minimiser des fonctions réelles différentiables. Cette approche itérative améliore successivement le point recherché en se déplacement dans la direction opposé au gradient de façon à faire décroître la fonction objectif. Dans sa version simple, l’algorithme trouve un minimum local (et pas global) et peut présenter certains inconvénients comme par exemple la difficulté à converger si le paramètre $\alpha$ (le pas de la descente) est mal réglé. Il existe tout une famille de méthodes dites à directions de descente qui exploitent le gradient pour converger le minimum de $f$ de façon plus efficace.

def gradient_descent(f, x0, gradient, alpha=0.01, itermax=1000):
    # initialization
    x, fx = np.zeros((itermax+1, len(x0))), np.zeros((itermax+1, 1))
    x[0,:] = x0
    # iterative loop
    k = 0
    while (k < itermax):
        grad_fxk = gradient(f, x[k,:]) # use analytical expression or numerical approximation
        x[k+1,:] = x[k,:] - alpha * grad_fxk
        k = k+1
    return x

Note: Si le pas de descente $\alpha$ est trop petit, l’algorithme risque de converger trop lentement (voir jamais). Si $\alpha$ est trop grand, l’algorithme peut diverger (notamment en zigzaguant dans les vallées étroites)

Nelder-Mead

image-right Un problème majeur des algorithmes à directions de descente est qu’elles sont surtout efficaces pour des fonctions différentiables et lorsqu’on connaît l’expression exacte du gradient de $f$. On peut néanmoins approximer le gradient par schéma numérique mais l’approximation faite rend souvent cette approche inefficace. La méthode de Nelder-Mead est une méthode qui exploite le concept de simplexe : une figure de $N+1$ sommets pour un espace à $N$ dimensions. L’idée consiste, à chaque itération, d’évaluer la valeur de la fonction $f$ à chaque point du simplexe et, selon ses valeurs, effectuer des transformations géométriques du simplexe (réflexion, expansion, contraction). Par exemple, dans une vallée, le simplexe sera étiré dans la direction où $f$ diminue. Bien que simple, cet algorithme permet de trouver un minimum sans calcul de gradient cependant il est moins efficace quand la dimension d’entrée $N$ est grande.

def nelder_mead(f, x0, params=2, itermax=1000):
    c = params   
    # initialization
    x1, x2, x3 = np.array([[x0[0]-0.5,x0[1]],[x0[0],x0[1]],[x0[0],x0[1]+0.5]])
    x  = np.array([x1, x2, x3])
    xm = np.zeros((itermax+1, len(x0)))
    # iterative loop
    k = 0
    while (k < itermax):
        # SORT SIMPLEX
        A = f(x.T)
        index = np.argsort(A) 
        x_min, x_max, x_bar = x[index[0],:], x[index[2],:], (x[index[0],:] + x[index[1],:])/2
        # REFLECTION
        x_refl = x_bar + (x_bar - x_max)
        # EXPANSION
        if f(x_refl) < f(x_min): 
            x_exp = x_bar + 2*(x_bar - x_max)
            if f(x_exp) < f(x_refl):
                x_max = x_exp
            else:
                x_max = x_refl
        elif (f(x_min) < f(x_refl)) and (f(x_refl) < f(x_max)):
            x_max = x_refl 
        # CONTRACTION
        else: 
            x_con = x_bar - (x_bar - x_max)/2
            if f(x_con) < f(x_min):
                x_max = x_con
            else:
                x[index[1],:] = x_max + (x[index[1],:] - x_min)/2
        # UPDATE DATAs
        x = np.array([x_max, x[index[1],:], x_min])
        xm[k+1,:] = x_bar
        k = k+1
    return xm[:k+1,:]

Attention: Comme la descente de gradient, la méthode de Nelder-Mead converge vers un minimum local de la fonction $f$ et non global. Il est toutefois possible de redémarrer l’algorithme avec une valeur d’initialisation $x_0$ différente pour espérer converger vers un nouveau minimum plus petit.

Stratégie d’évolution

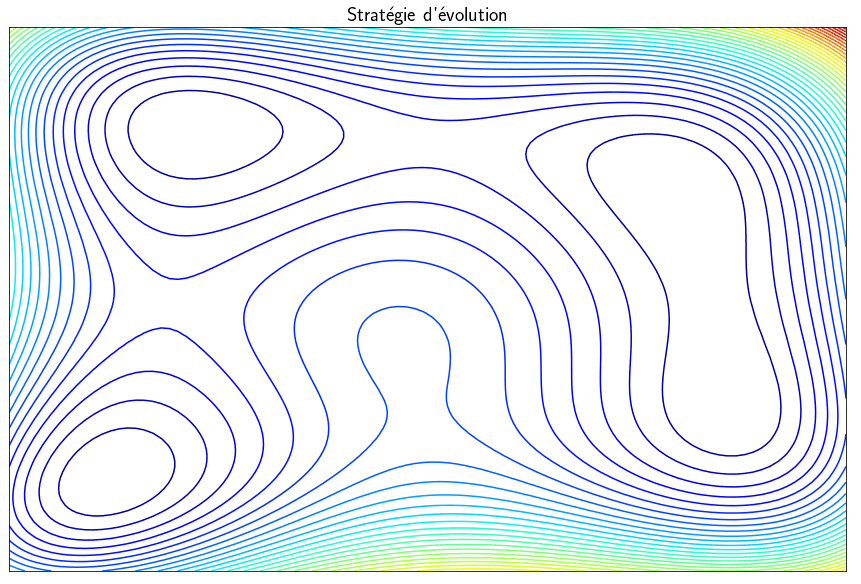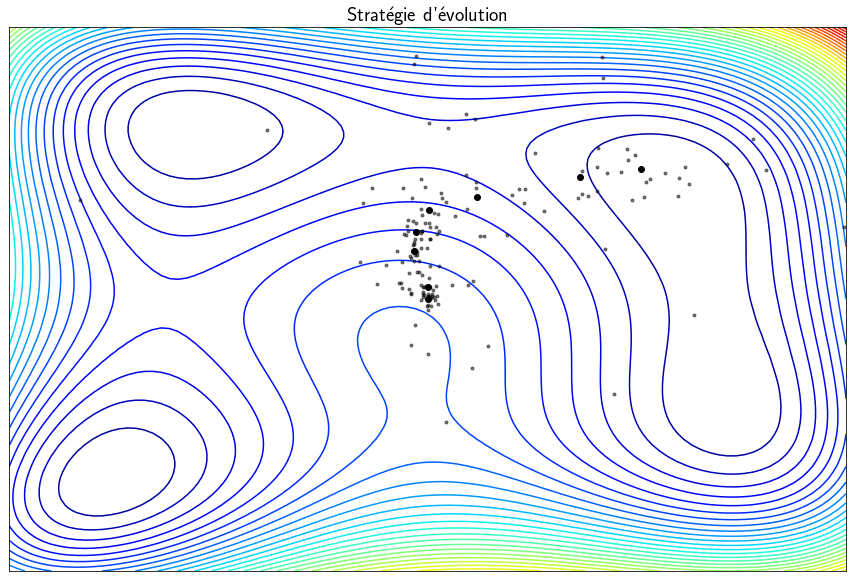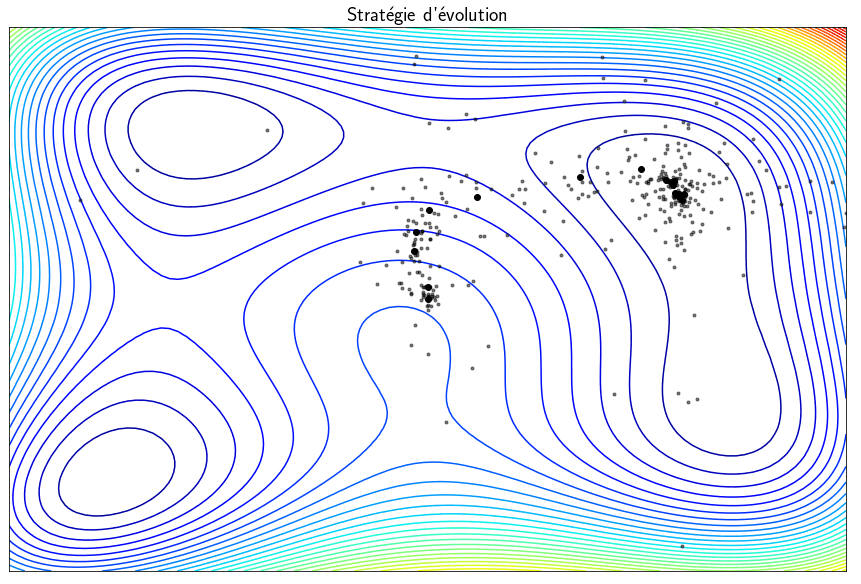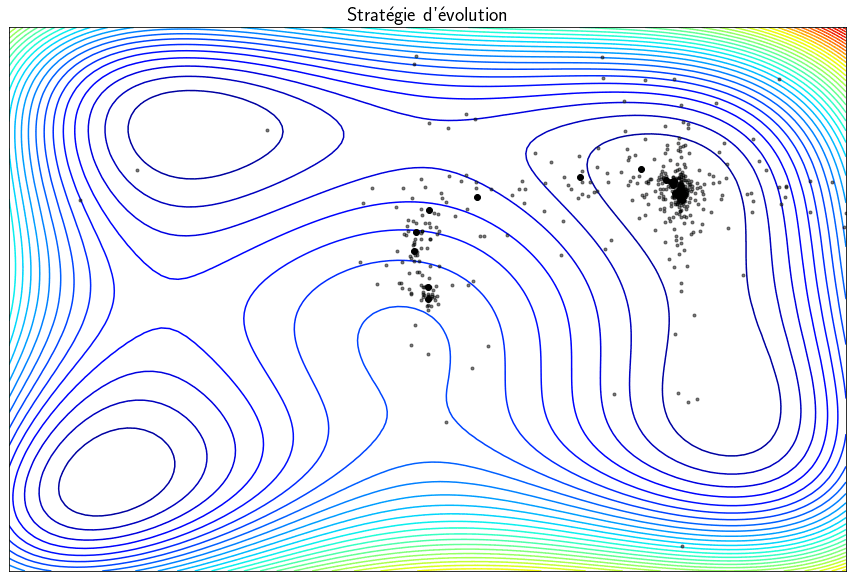image-right Les méthodes présentées précédemment sont capables de trouver des minima mais des minima locaux et non globaux. Les techniques dites stratégies d’évolution sont des métaheuristiques inspirées de la théorie de l’évolution qui converge statistiquement vers un minimum global. L’idée est de partir d’une population de $\mu$ parents qui vont produire $\lambda$ enfants. Parmis ces $\lambda$ enfants, seuls ceux les mieux sont sélectionné pour faire partie de la prochaine génération. Le vocabulaire utilisé est celui de l’évolution mais, en pratique, on fait des tirages aléatoires de points et on garde ceux pour lesquelles la fonction $f$ est minimale. This algorithm can find a global minimum but the main drawback is that it requires a large number of evaluations of the function $f$ which is generally computationally expensive.

def evolution_strategy(f, x0, params=[5,3,1], imax=1000):
    # parameters
    dim = len(x0)
    lambd, mu, tau = params
    # initialization
    x, xp, s = np.zeros((imax+1, dim)), np.zeros((imax+1, lambd, dim)), np.zeros((imax+1, dim))
    x[0,:] = x0
    s[0,:] = [0.1,0.1]
    # ITERATIVE LOOP
    k = 0
    while (k < imax):
        # GENERATION
        sp = s[k,:] * np.exp(tau * randn(lambd, dim))
        xp[k,:,:] = x[k,:] + sp * randn(lambd, dim)
        Zp = [f(xi) for xi in xp[k,:,:]]
        # SELECTION
        mins = np.argsort(Zp)[:mu]
        xc   = xp[k,mins,:]
        sc   = sp[mins,:]
        # UPDATE
        x[k+1,:] = np.mean(xc, 0)
        s[k+1,:] = np.mean(sc, 0)
        k = k+1
    return x[:k+1,:]

Problème d’aérodynamisme

Imaginons qu’on veuille créer un avion d’un poids de $P=6 kg$ et qui aura une vitesse moyenne de vol de $V=12 m/s$, le problème est de designer les ailes de l’avion de telle façon que l’énergie qui sera dépensée soit minimum. Si on considère un vol stationnaire, il existe 4 forces principales qui s’opposent : la poussée (produit par les moteurs), la trainée ( due à la résistance de l’air, le profil de l’aile, la compressibilité …), le poids (gravité terrestre), et la portance (plus d’infos chez science étonnante). Le but de notre problème d’optimisation du profil d’aile est donc de trouver une forme d’aile qui minimisera la trainée et maximisera la portance. La portance verticale $F_y$ d’une aile et la trainée horizontale $F_x$ sont calculées grâce aux formules suivantes issues de la mécanique des fluides :

\[F_y = \frac{1}{2}\, \rho\, S\, V^2\, C_y \quad \text{et} \quad F_x = \frac{1}{2}\, \rho\, S\, V^2\, C_x\]

avec

$\rho$ la masse volumique de l’air ($kg/m^3$)
$S$ la surface de l’aile ($m^2$)
$V$ la vitesse ($m/s$)
$C_y$ le coefficient de portance
$C_x$ le coefficient de trainée

Finalement, la fonction à minimiser s’écrit :

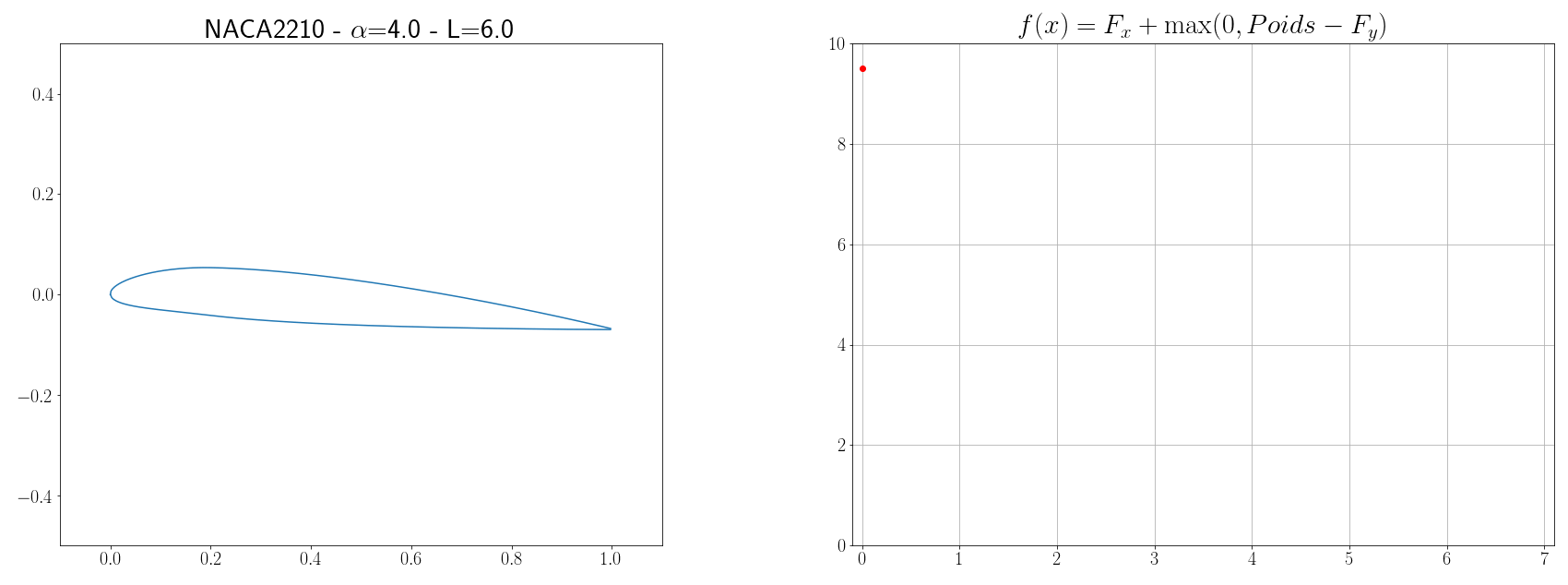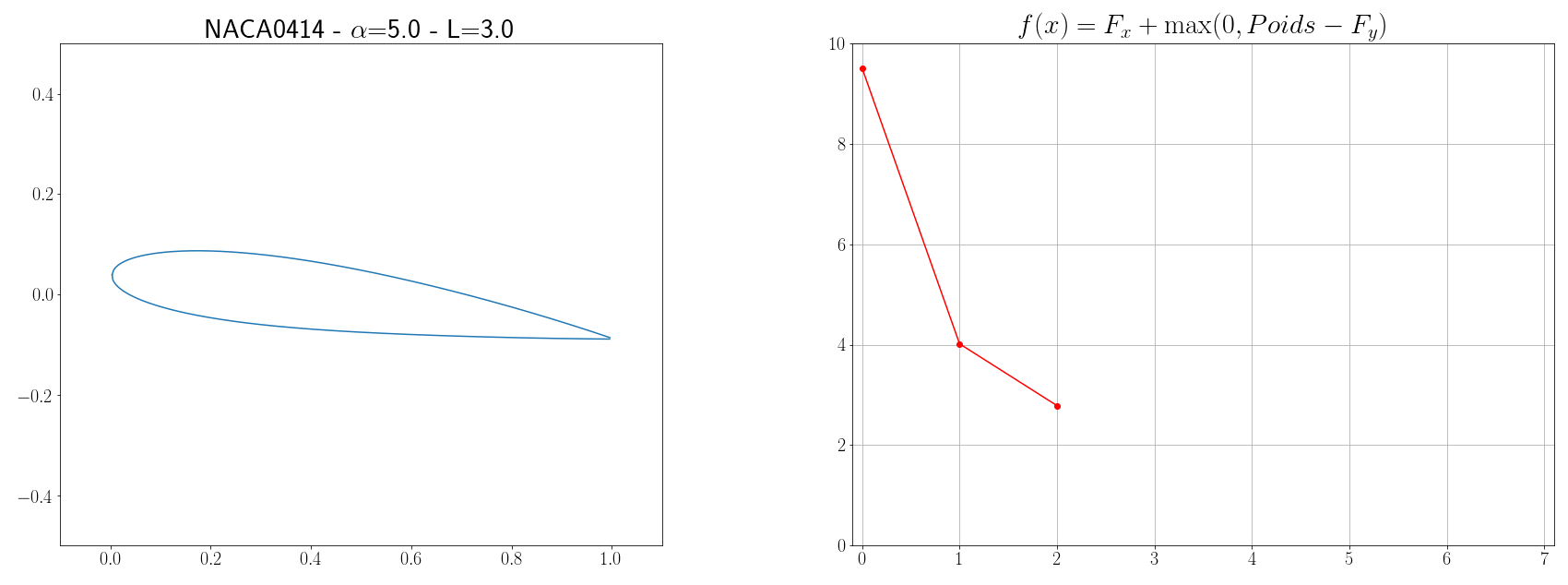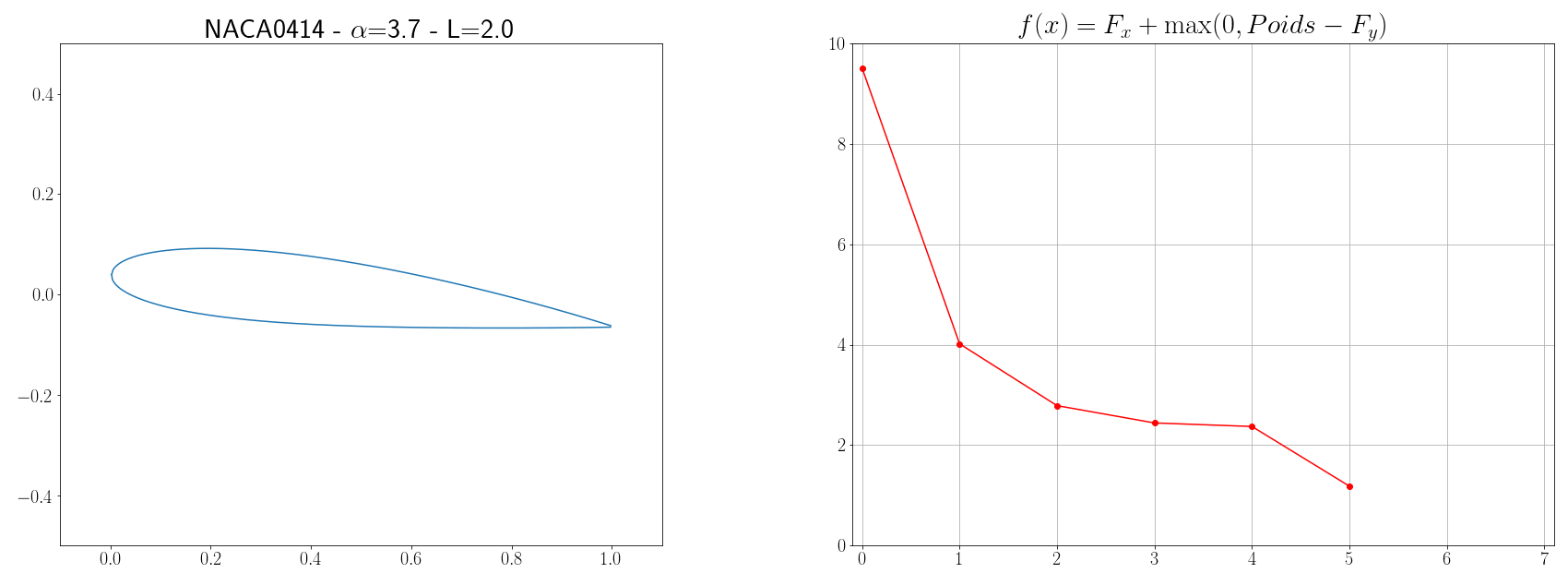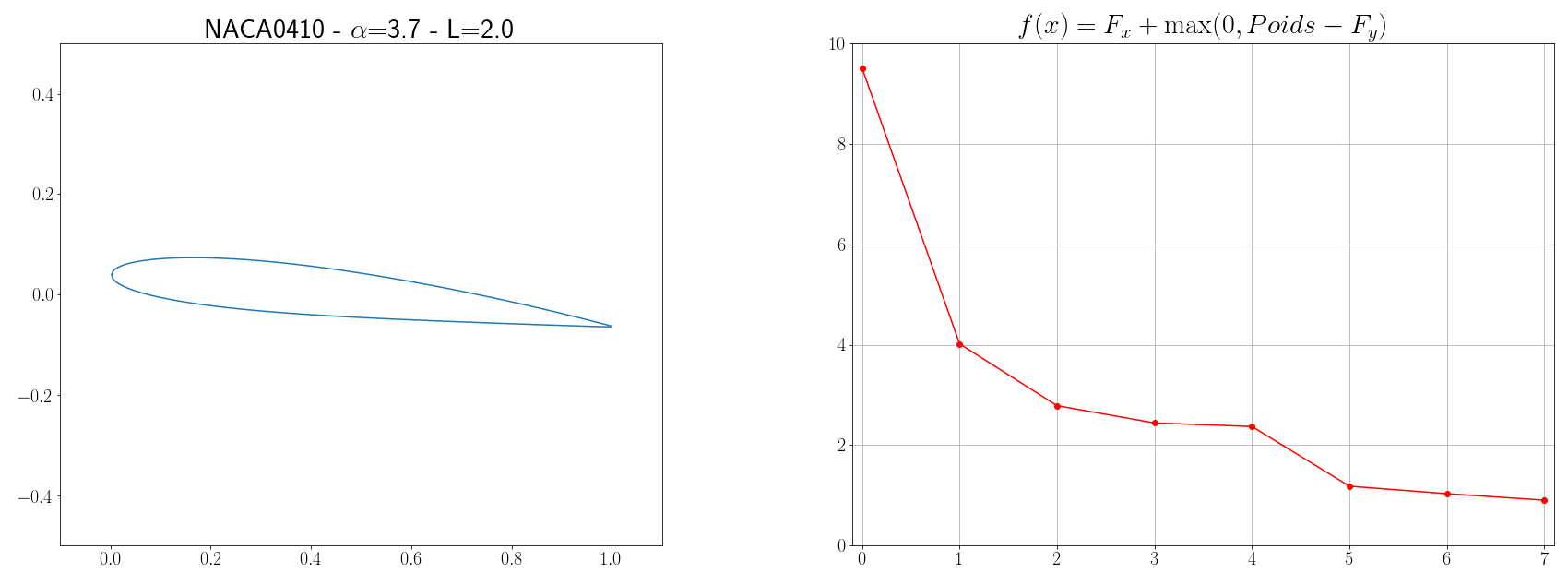
\[f(x) = F_x + \max(0, P - F_y)\]

avec $x = \left[ \text{NACA}_{M} \text{, NACA}_{P} \text{, NACA}_{XX} \text{, L, }\alpha \right]$

# constantes
poids = 6
Ro    = 1
V     = 12
# function to minimize
def cost_function(x):
    # call xfoil
    write_xfoil(x)
    os.system(r'xfoil.exe < input.dat')
    CL, CD = read_xfoil()
    # compute COST function
    L  = x[3]
    c  = (1/10)*L
    S  = L*c
    Fx = 0.5*Ro*S*V**2*CD
    Fy = 0.5*Ro*S*V**2*CL
    y  = Fx + max(0, poids-Fy)
    return y

Les paramètres à trouver définissant la forme de l’aile sont la géométrie du profil, l’envergure $L$ de l’aile et l’angle d’attaque $\alpha$. La géométrie du profil peut être définie par le code NACA MPXX où M est la cambrure maximale, P le point de cambrure maximal par rapport au bord d’attaque de la corde, et XX l’épaisseur maximale du profil. Par exemple, le profil aérodynamique NACA 2412 possède une cambrure maximale de $2%$ à $40%$ à partir du bord d’attaque avec une épaisseur maximale de 12%. D’autres part, pour simplifier, on supposera que la corde est 10 fois plus petite que l’envergure de l’aile. Ensuite, pour pouvoir évaluer les forces $F_x$ et $F_y$, il est nécessaire de connaître les coefficients $C_y$ et $C_x$. Ces coefficients dépendent de la forme de l’aile ainsi que de grandeurs physiques comme le nombre de Mach $Ma = \frac{v}{a} = \frac{12}{340}$ et le nombre de Reynolds $Re = \frac{\rho v L}{\mu} = \frac{12L}{1.8 10^{-5}}$, l’estimation de $C_x$ et $C_y$ n’est pas un problème évident. Mais des solveurs aérodynamiques comme XFOIL implémentent des outils pour calculer ces coefficients (cf page 16). L’idée est donc d’executer des commandes XFOIL et de récupérer sa sortie à chaque fois que la fonction coût $f$ doit être évaluée.

def read_xfoil():
    with open("results.dat", "r") as file:
        coeffs = file.readlines()[-1]
    CL = float(coeffs.split()[1])
    CD = float(coeffs.split()[2])
    return CL, CD

def write_xfoil(x):
    NACAx, NACAy  = int(x[0]), int(x[1])
    NACAep, alpha = int(x[2]), x[4]
    corde    = (1/10)*x[3]
    mach     = 12/340
    reynolds = corde*12./(1.8*10e-5)
    # write command in file
    file = open("input.dat", "w")
    file.write("plop\ng\n\n")
    file.write("naca "+str(NACAx)+str(NACAy)+str(NACAep)+"\n\noper\n")
    file.write("mach "+str(mach)+"\n")
    file.write("visc "+str(reynolds)+"\n")
    file.write("pacc\nresults.dat\ny\n\n")
    file.write("alfa "+str(alpha)+"\n\nquit")
    file.close()

Maintenant qu’on est capable de calculer la fonction $f$ à minimiser, on peut appliquer un algorithme d’optimisation. Étant que les méthodes présentées dans la section précédente sont basiques, il n’y a pas de honte à utiliser directement des librairies comme Scipy qui implémente la métaheuristique du recuit simulé (s’inspire de processus métallurgique). Scipy possède plusieurs autres algorithmes d’optimisation mais, après expériences, c’est celui-ci qui semblait être le plus efficace.

from scipy import optimize
x0 = np.array([2, 4, 12, 5, 5])
bounds = [(0,4),(2,8),(10,20),(2,6),(0,10)]
optimize.dual_annealing(cost_function, bounds, x0=x0, maxiter=10)

Julien Guégan