Réseau de Neurone : statistique, gradient, perceptron

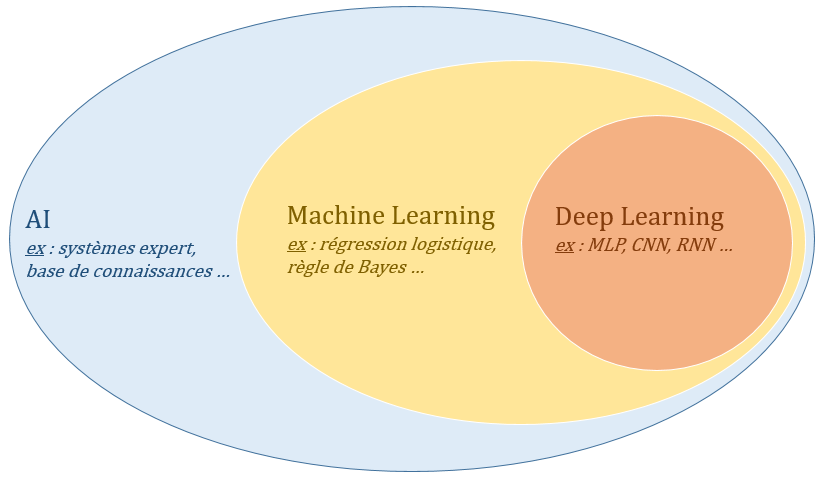
Ces dernières années, on entend de plus en plus dans les médias les mots : intelligence artificielle, réseau de neurone, Deep Learning … En effet, de nombreuses innovations ont emmergées grâce à ces technologies mais que ce cache-t-il vraiment derrière cette terminologie ? Depuis que les premiers ordinateurs programmables ont été conçus, les gens ont été étonnés de voir ces ordinateurs résoudre des tâches impossibles pour tout être humain. Cependant, ces problèmes étaient en fait faciles à décrire par une liste formelle de règles mathématiques. Le vrai challenge pour les ordinateurs est d’effectuer des tâches que les humains réalisent facilement et intuitivement mais qu’ils ont beaucoup plus de mal à décrire formellement comme, par exemple, reconnaître un langage ou des visages. De nos jours, on appelle intelligence artificielle (IA) toute technique permettant de résoudre un problème plus ou moins complexe par le biais d’une machine. Le Machine Learning et le Deep Learning sont des champs d’étude de l’IA fondés sur des théories statistiques.

Apprentissage Statistique

L’apprentissage statistique (ou Machine Learning en anglais) se concentre sur l’étude des algorithmes permettant aux ordinateurs d’apprendre à partir des données et d’améliorer leur performances à résoudre des tâches sans avoir explicitement programmée chacune d’entre elles. Soit un ensemble $(x_i,y_i)$ de $n$ données d’apprentissage (avec $x_i$ une donnée et $y_i$ sa classe). Le but de l’apprentissage supervisé est de déterminer une estimation $h$ de $f$ en utilisant les données $(x_i,y_i)$ à disposition. On distingue alors deux types de prédictions selon la nature de $Y$ : si $Y \subset \mathbb{R}$, on parle de problème de régression et si $Y = {1,…,I}$ on parle de problème de classification. Pour estimer la loi $f$, une approche classique est la minimisation du risque empirique. Étant donné une fonction loss $L(\hat{y},y)$ (aussi appelé fonction de coût, de perte, objectif) qui mesure à quel point la prédiction $\hat{y}$ d’un modèle $h$ est différente de la vraie classe $y$ alors le risque empirique est :

\[R_{emp}(h) = \frac{1}{n} \sum_{i=1}^n L\left(h(x_i),y_i\right)\]

Le principe de minimisation du risque empirique dit que l’algorithme d’apprentissage doit choisir un modèle $\hat{h}$ qui minimise ce risque empirique : $ \hat{h} = \arg \min_{h \in \mathcal{H}} R_{emp}(h) $. L’algorithme d’apprentissage consiste donc à résoudre un problème d’optimisation. La fonction à minimiser est une approximation d’une probabilité inconnue, elle est faite en moyennant les données à disposition et plus ces données seront nombreuses plus elle l’approximation sera juste. À propos de la fonction loss $L(\hat{y},y)$, on peut en théorie utiliser la fonction 0-1 loss pour pénaliser les erreurs et ne rien faire sinon :

\[L(\hat{y},y) = \left\{ \begin{array}{ll} 1 & \text{si } \hat{y} \neq y \\ 0 & \text{si } \hat{y} = y \end{array} \right.\]

Mais, en pratique, il est préférable d’avoir une fonction loss continue et différentiable pour l’algorithme d’optimisation. Par exemple, la mean squared error (MSE) qui est souvent choisie pour des problèmes de regression, par exemple pour un cas linéaire où l’on veut trouver la meilleure droite passant par des points. Cependant, la MSE a le désavantage d’être dominée par les outliers qui peuvent faire tendre la somme vers une valeur élevée. Une loss fréquemment utilisée en classification et plus adaptée est la cross-entropie (CE) :

\[MSE = (y - \hat{y})^2 \quad \quad \quad CE = - y \log(\hat{y})\]

def compute_loss(y_true, y_pred, name):
    if name == 'MSE':
        loss = (y_true - y_pred)**2
    elif name == 'CE':
        loss = -(y_true * np.log(y_pred) + (1-y_true) * np.log(1-y_pred))
    return loss.mean()

Note: Pour résoudre ce problème de minimisation, le plus efficace est d’utiliser un algorithme de descente de gradient (cf post précédent) mais nécessite de connaître la dérivée exacte de la fonction Loss. Les librairies récente de Deep Learning (Pytorch, Tensorflow, Caffe …) implémentent ces algorithmes d’optimisation ainsi que des frameworks d’auto-différentation

Maintenant que la notion d’apprentissage a été définie, l’élément le plus important est de construire un modèle $h$ capable de classifier ou régresser des données. L’un des modèles parmis les plus connues de nos jours est celui des réseaux de neurones.

Réseaux de Neurones

Perceptron

Le premier modèle à l’origine des réseaux de neurones est le Perceptron (F. Rosenblatt,1957), il peut être vu comme un unique et simple neurone qui résout un problème de classification linéaire. Le Perceptron transforme un vecteur d’entrée $X=(x_1,…,x_d) \in \mathbb{R}^d$ en une sortie $Y \in [0,1]$, l’étiquette de classification. L’idée est qu’on cherche à séparer notre espace d’entrée en 2 régions par un hyperplan $\mathcal{H}$ définit simplement par :

\[\mathcal{H} : w^T X + b = 0 \iff \mathcal{H} : \sum_{i=1}^d w_i x_i + b = 0\]

où $w=(w_1,…,w_d) \in \mathbb{R}^d$ et $b \in \mathbb{R}$ sont les paramètres de l’hyperplan $\mathcal{H}$ qu’on appelle communément les poids du neurone.

class Perceptron:
    
    def __init__(self, n_inputs, n_iter=30, alpha=2e-4):
        self.n_iter = n_iter # number of iterations during training
        self.alpha  = alpha # learning rate
        self.w      = np.zeros((n_iter, n_inputs+1))
        self.w[0,:] = np.random.randn(n_inputs+1) # weights and bias parameters

    def predict(self, X, i=-1): 
        return np.sign(X @ self.w[i,1:] + self.w[i,0]) 

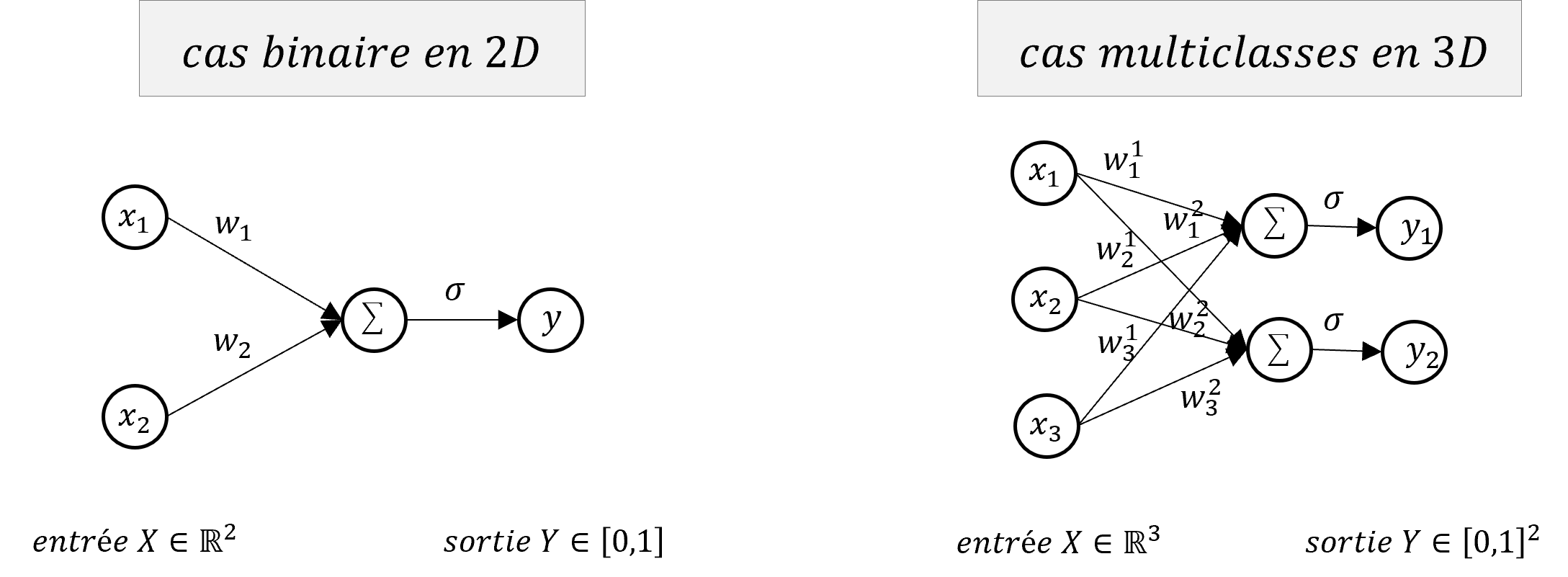
Cet hyperplan sépare donc l’espace en 2 et est donc capable de classifier un donnée $X$ en créant une règle comme $ f(X) = 1 \ \text{si } w^T X + b<0 \ ; 0 \text{ sinon} $. Notre modèle de neurone se résume donc à des paramètres modélisant un hyperplan et une règle de classification. Dans notre paradigme du machine learning, on suppose qu’on a, à notre disposition, un ensemble de $n$ données étiquetées $(X,Y) \in \mathbb{R}^{n\times d} \times [0,1]^n$. Comme expliqué dans la section précédentes, la phase d’apprentissage consiste à minimiser l’erreur de classification que fait le modèle sur ces données et ajuster les paramètres $w$ et $b$ qui permettent au modèle du Perceptron de séparer correctement ces données.

    def gradient_descent(self, i, y, y_pred):
        # construct input X and 1 to have bias
        inputs = np.hstack((np.ones((X.shape[0], 1)), X))
        # compute gradient of the MSE loss
        gradient_loss = -2 * np.dot(y_true - y_pred, inputs)
        # apply a step of gradient descent
        self.w[i+1,:] = self.w[i, :] - self.alpha * gradient_loss

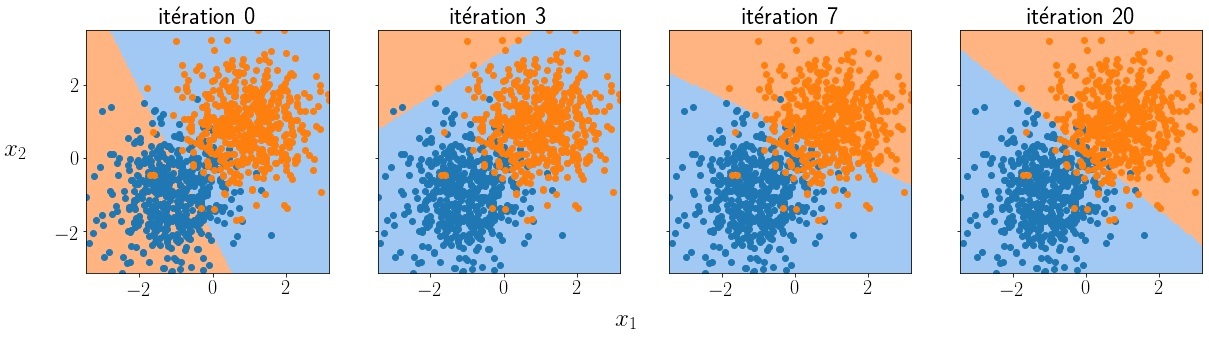
Ci-dessus, la loss MSE a été utilisée. Sa dérivée exacte en fonction de $w$ peut se calculer facilement (cf ci-dessous).

$$ L = \frac{1}{n}\sum_{i=1}^n (y_i - \hat{y}_i)^2 = \frac{1}{n}\sum_{i=1}^n (y_i - (w_i x_i + b))^2 \\[5pt] \left\{ \begin{array}{ccc} \dfrac{\partial L}{\partial w} &=& \dfrac{\partial}{\partial w} \dfrac{1}{n} \sum_{i=1}^n (y_i - (w_i x_i + b))^2 \\[10pt] \dfrac{\partial L}{\partial b} &=& \dfrac{\partial}{\partial b} \dfrac{1}{n} \sum_{i=1}^n (y_i - (w_i x_i + b))^2 \\ \end{array} \right. \\[10pt] \left\{ \begin{array}{cc} \dfrac{\partial L}{\partial w} &=& -\dfrac{2}{m}\sum_{i=1}^{m}(y_i - w_i x_i - b)x_i \\[10pt] \dfrac{\partial L}{\partial b} &=& -\dfrac{2}{m}\sum_{i=1}^{m}(y_i - w_i x_i - b) \end{array} \right. \\[10pt] \left\{ \begin{array}{cc} \dfrac{\partial L}{\partial w} &=& -\dfrac{2}{m}\sum_{i=1}^{m}(y_i - \hat{y}_i)x_i \\[10pt] \dfrac{\partial L}{\partial b} &=& -\dfrac{2}{m}\sum_{i=1}^{m}(y_i - \hat{y}_i) \end{array} \right. \\ $$ En python, on a rajouté 1 à l'entrée X pour prendre en compte l'équation du biais. Le gradient s'écrit bien `gradient_loss = -2 * np.dot(y_true - y_pred, inputs)`

Notez que ce modèle est très proche d’une simple régression linéaire mais présenté ici pour un problème de classification, on peut facilement l’adapter à une régression en supprimant la fonction np.sign() dans le code python. D’autres part, le problème résolu ici est binaire (on a 2 classes) mais on peut facilement étendre le modèle pour qu’il prédise plusieurs classes en remplaçant le vecteur de poids $w \in \mathbb{R}^d$ par une matrice $W \in \mathbb{R}^{d \times c}$ représentant donc plusieurs hyperplans séparateurs où $c$ est le nombre de classes possible, la sortie du modèle $Y$ n’est plus un scalaire mais alors un vecteur de $\mathbb{R}^c$. Enfin, on notera qu’en pratique, la fonction de classification $f$ est remplacée par une fonction différentiable $\sigma : \mathbb{R} \rightarrow [0,1]$. Pour un problème binaire, la fonction sigmoïde $\sigma(z)=\frac{1}{1+e^{-z}}$ est utilisée puis la classe est choisie selon un seuil (ex : $\sigma(z) > 0.5$). Pour un cas multi-classe, la fonction de classification est une fonction softmax $\sigma(z_j)=\frac{e^{z_j}}{\sum_{k=1}^Ke^{z_k}}$ qui retourne un vecteur de pseudo-probabilité (somme à 1) et la classe retenue est choisie en gardant la position de la valeur maximum du vecteur.

Perceptron Multi-Couches

Comme décrit ci-dessus, un neurone unique peut résoudre un problème linéairement séparable mais échoue lorsque les données ne sont pas linéairement séparable. Pour approximer des comportements non linéaires, l’idée est d’ajouter notamment des fonctions non linéaires dans le modèle, elles sont appelées fonctions d’activation (cf exemples ci-dessous).

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def relu(x):
    return x * (x > 0)

def tanh(x):
    return np.tanh(x)

Le modèle du réseau de neurones ou Perceptron Multi-Couches consiste à enchaîner successivement plusieurs transformations linéaires effectuées par des neurones simples et des transformations non linéaires réalisées par ces fonctions d’activations jusqu’à la dernière opération qui retournera la classe prédite par le modèle. Une couche $l$ du réseau de neurone est alors composée de $m$ neurones modélisés par une matrice de poids $W^l \in \mathbb{R}^{(d+1)\times m}$ (par simplicité on intègre le biais $b$ dans $W$) ainsi que d’une fonction d’activation $A^l$. Au final, le réseau de neurone complet peut être décrit par une combinaison de composition de fonctions et multiplications matricielles en allant de la 1ère couche à la dernière :

\[h(X) = \hat{Y} = A^l(W^l A^{l-1}(W^{l-1} \cdots A^0(W^0 X)\cdots))\]

class MultiLayerPerceptron:
    ''' MLP model with 2 layers '''

    def __init__(self, n_0, n_1, n_2):
        # initialize weights of 1st layer (hidden) and 2nd layer (output)
        self.W1 = np.random.randn(n_0, n_1)
        self.b1 = np.zeros(shape=(1, n_1))
        self.W2 = np.random.randn(n_1, n_2)
        self.b2 = np.zeros(shape=(1, n_2))        

    def forward(self, X):
        # input
        self.A0 = X
        # first layer
        self.Z1 = np.dot(self.A0, self.W1) + self.b1
        self.A1 = relu(self.Z1)
        # second layer
        self.Z2 = np.dot(self.A1, self.W2) + self.b2
        self.A2 = sigmoid(self.Z2)
        # output
        y_pred = self.A2
        return y_pred

Note: Notez qu’on peut construire un réseau avec autant de couches cachées que l’on veut et que chacunes de ces couches peuvent être constituées également d’un nombre arbitraire de neurones et ce peu importe la dimension d’entrée et de sortie du problème.

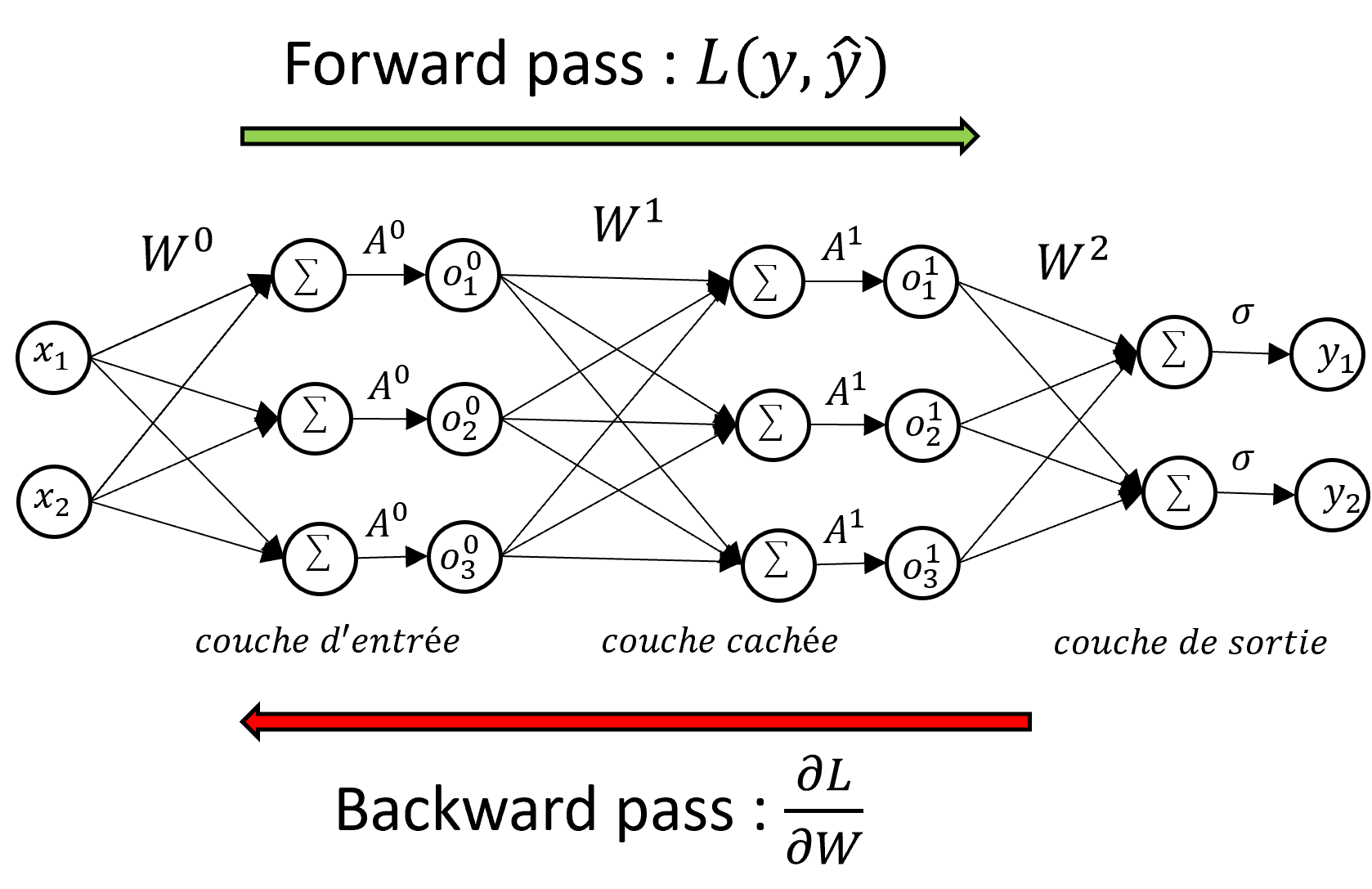
Cet enchaînement de couches de neurones pose problème pour la phase d’entraînement : le calcul de $\frac{\partial\mathcal{L}}{\partial W}$ est moins trivial que pour le modèle du neurone formel puisqu’il faut prendre en compte les poids $W^l$ de chaque couche $l$. La technique de la rétropropagation du gradient permet d’entraîner des réseaux de neurones multi-couches en se basant sur la règle de dérivation en chaîne. Le gradient de la loss est calculé en utilisant les dérivées des poids des neurones et leur fonction d’activation en partant de la dernière couche jusqu’à la première couche. Il faut donc parcourir le réseau vers l’avant (forward pass) pour obtenir la valeur de la loss puis vers l’arrière (backward pass) pour obtenir la valeur de la dérivée de la loss nécessaire à l’algorithme d’optimisation. Si on s’intéresse au neurone $j$ de la couche $l$ vers le neurone $i$ de la couche $l+1$, on note $a$ la valeur du produit vectoriel, $o$ la sortie du neurone (après activation) et qu’on garde le reste des notations précédentes, le calcul du gradient de $L$ en fonction de $W$ est :

\[\begin{align*} \dfrac{\partial L}{\partial w_{ij}^l} &= \underbrace{\quad \dfrac{\partial L}{\partial a_{j}^l} \ \ } \ \ \underbrace{\quad \dfrac{\partial a_j^l}{\partial w_{ij}^l} \quad} \\ & \qquad \ \ \ \delta_j^l \quad \ \ \ \dfrac{\partial}{\partial w_{ij}^l} \sum_{n=0}^{N_{l-1}} w_{nj}^l o_n^{l-1} = o_i^{l-1} \end{align*}\]

On a donc que la dérivée $\dfrac{\partial L}{\partial w_{ij}^l}$ dépend du terme $\delta_j^l$ de la couche $l$ et de la sortie $o_i^{l-1}$ de la couche $l-1$. Ça fait sens puisque le poids $w_{ij}^l$ connecte la sortie du neurone $i$ dans la couche $l-1$ à l’entrée du neurone $j$ dans la couche $l$. On développe maintenant le terme $\delta_j^l$ :

\[\delta_j^l = \dfrac{\partial L}{\partial a_{j}^l} = \sum_{n=1}^{N_{l+1}} \dfrac{\partial L}{\partial a_n^{l+1}}\dfrac{\partial a_n^{l+1}}{\partial a_j^l} = \sum_{n=1}^{N_{l+1}} \delta_n^{l+1} \dfrac{\partial a_n^{l+1}}{\partial a_j^l}\]

or, on a :

\[\begin{align*} & a_n^{l+1} &=& \sum_{n=1}^{N_{l}} w_{jn}^{l+1}A(a_j^l) \\ \Rightarrow & \dfrac{\partial a_n^{l+1}}{\partial a_j^l} &=& \ w_{jn}^{l+1}A'(a_j^l) \end{align*}\]

et donc :

\[\dfrac{\partial L}{\partial w_{ij}^l} = \delta_j^l o_i^{l-1} = A'(a_j^l) o_i^{l-1} \sum_{n=1}^{N_{l+1}} w_{jn}^{l+1} \delta_n^{l+1}\]

On obtient donc que la dérivée partielle de $L$ par rapport à $w_{ij}$ à la couche $l$ dépend également de la dérivée à la couche $l+1$. Pour calculer la dérivée de tout le réseau en utilisant la règle de la dérivation en chaîne, il est donc nécessaire de commencer par la dernière couche pour finir par la première d’où le terme de backpropagation de l’erreur.

Attention: Comme les calculs de la phase de backpropagation dépendent également de $a_j^l$ et $o_i^{l-1}$, il faut faire d’abord une pass forward avant la pass backward pour stocker ces valeurs en mémoires.

''' training methods for 2 layer MLP and cross-entropy loss '''
    def backward(self, X, y):
        m = y.shape[0]
        self.dZ2 = self.A2 - y
        self.dW2 = 1/m * np.dot(self.A1.T, self.dZ2)
        self.db2 = 1/m * np.sum(self.dZ2, axis=0, keepdims=True)
        self.dA1 = np.dot(self.dZ2, self.W2.T)
        self.dZ1 = np.multiply(self.dA1, d_relu(self.Z1))
        self.dW1 = 1/m * np.dot(X.T, self.dZ1)
        self.db1 = 1/m * np.sum(self.dZ1, axis=0, keepdims=True)

    def gradient_descent(self, alpha):
        self.W1 = self.W1 - alpha * self.dW1
        self.b1 = self.b1 - alpha * self.db1
        self.W2 = self.W2 - alpha * self.dW2
        self.b2 = self.b2 - alpha * self.db2

Note: Lors de l’apprentissage, on optimise seulement les poids $W$ du modèle. Le nombre de couches cachées ainsi que le nombre de neurones par couche sont fixes et ne changent pas. On parle d’hyperparamètres, il faut les choisir lors de la conception du modèle. Des techniques de recherches d’hyperparamètres optimaux existent mais sont complexes et gourmandes en temps de calcul.

Aller plus loin

La popularité des réseaux de neurones ces dernières années n’est en réalité pas due au modèle du MLP présenté jusqu’à présent. En effet, l’inconvénient principal du MLP est le grand nombre de connexion existant entre chaque neurone qui entraîne une forte redondance et une difficulté à l’entrainement lorsque le nombre de neurone et de dimension d’entrée sont élevés.

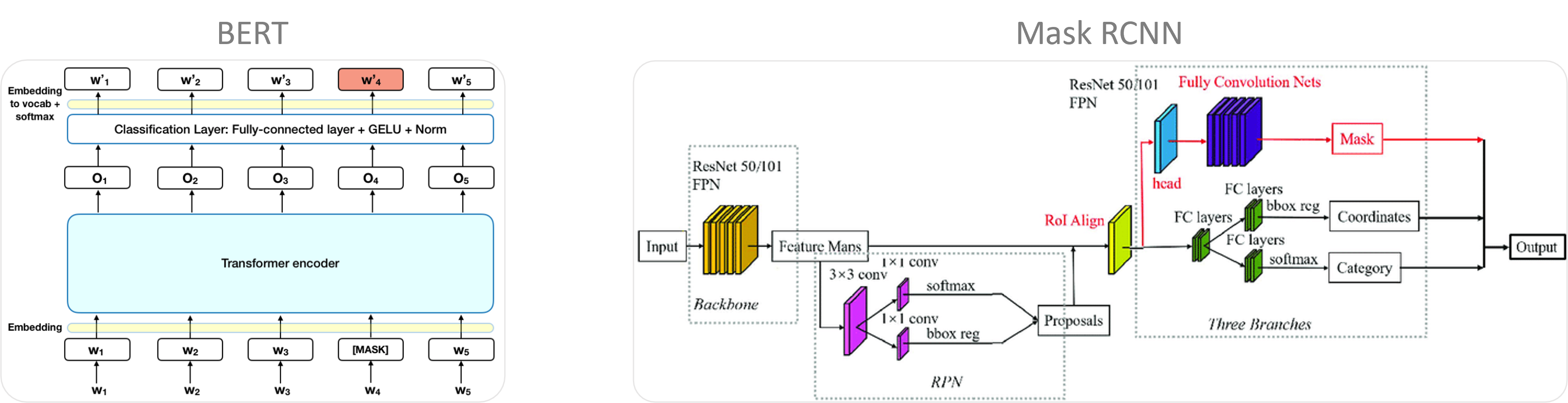
Sur des problèmes complexes comme l’analyse d’image, le traitement de texte ou le traitement de la parole, l’efficacité des réseaux de neurones actuels est, en majorité, due à des opérations et des connexions plus avancées qui permettent de modéliser et représenter efficacement ces problèmes. Par exemple, pour les images, des opérateurs de convolution sont exploités, ils tirent parti de la structure locale des pixels pour comprendre les informations présentes, allant de formes simples (lignes, cercles, couleur …) à plus complexes (animaux, bâtiment, paysages …). Pour des données séquentielles, les connexions LSTM (long short-term memory) sont capables de mémoriser des données importantes passées en évitant les problèmes de disparition de gradient. D’autres parts, de nombreuses techniques existent pour améliorer la phase d’apprentissage et avoir des performances qui généralisent le modèle à des données dites de test jamais vues par le modèle lors de l’entraînement (augmentation de données, dropout, early stopping …).

---