CNN : convolution, Pytorch, Deep Dream

9 minute(s) de lecture

Les réseaux de neurones convolutionnels (CNN) sont les modèles qui ont permis de faire un bon en avant dans les problèmes de reconnaissance d’image. Ils sont au coeur de nombreuses applications allant des systèmes de sécurité par identification faciale à la classification de vos photos de vacances en passant par la génération synthétique de visage et les filtres snapchat. L’un des fondateurs de ce modèle est Yann Le Cun (un français !) qui, en 1989, applique la backpropagation du gradient pour apprendre des filtres de convolution et permet à un réseau de neurone à reconnaître des chiffres manuscrits. Cependant, c’est seulement en 2012 que les CNN se répandent largement dans la communauté scientifique de la vision par ordinateur avec Alex Krizhevsky qui conçoit l’architecture AlexNet et remporte la compétition ImageNet Large Scale Visual Recognition Challenge (1 million d’images de 1000 classes différentes) en implémentant son algorithme sur des GPUs ce qui permet au modèle d’apprendre rapidement d’une grande quantité d’image. Ce modèle atteint des performances 10% plus élevées que tous les autres à cette époque et il est désormais l’un des papiers publiés les plus influents en Computer Vision (en 2021, plus de 80 000 citations selon Google Scholar).

Convolutions et Réseaux de neurones

Les modèles de réseaux de neurones complètements connectés (cf post précédent) ne sont pas adaptés pour résoudre des problèmes de traitement d’image. En effet, les MLP ont chaque neurone d’une couche connecté à chaque unité d’entrée : le nombre de paramètre à apprendre devient vite élevé et une forte redondance dans les poids du réseau peut exister. De plus, pour utiliser une image dans un tel réseau, tous les pixels devrait être transformée en vecteur et aucune information sur la structure locale des pixels serait alors prise en compte.

Le produit de convolution, noté $\ast$, est un opérateur qui généralise l’idée de moyenne glissante. Il s’applique aussi bien à des données temporelles (en traitement du signal par exemple) qu’à des données spatiales (en traitement d’image). Pour le cas des images, c’est-à-dire discret et en 2 dimensions, la convolution entre une image $I$ et un noyau $w$ (ou kernel) peut se calculer comme suit :

\[I(i,j) * \omega =\sum_{x=-a}^a{\sum_{y=-b}^b{ I(i+x,j+y)} \ \omega(x,y)}\]

L’idée est de faire glisser le noyau spatialement sur toute l’image et à chaque fois de faire une moyenne pondérée des pixels de l’image se retrouvant dans la fenêtre concernée par les éléments du noyau. Selon la valeur des éléments du noyau de convolution $w$, l’opération peut mettre en avant des caractéristiques particulières se trouvant dans l’image comme des contours, des textures, des formes.

Remarque: Il existe plusieurs paramètres associés à l’opération de convolution comme la taille du noyau utilisé, la taille du pas lorsqu’on fait glisser la fenêtre sur l’image, la façon dont on gère les bords de l’image, le taux de dilatation du noyau … plus d’infos ici

On peut par exemple mettre en avant les pixels d’une image correspondants aux contours horizontaux en appliquant une convolution avec un noyau de taille $3 \times 3$ avec des $-1$ dans la 1ère ligne, des $0$ dans la 2ème ligne et des $+1$ dans la 3ème ligne de la matrice.

import matplotlib.pyplot as plt
import numpy as np
from scipy.signal import convolve2d
# read image
image = np.array(Image.open("path/to/file.jpg").convert('L'))
# apply convolution
kernel = np.array([[-1, -1, -1],
                   [ 0,  0,  0],
                   [+1, +1, +1]])
conv_output = convolve2d(image, kernel, mode='same')
# display
plt.figure(figsize=(15,5))
plt.subplot(121), plt.imshow(image, cmap='gray'), plt.axis('off')
plt.subplot(122), plt.imshow(np.abs(conv_output), cmap='gray'), plt.axis('off')
plt.tight_layout()
plt.show()

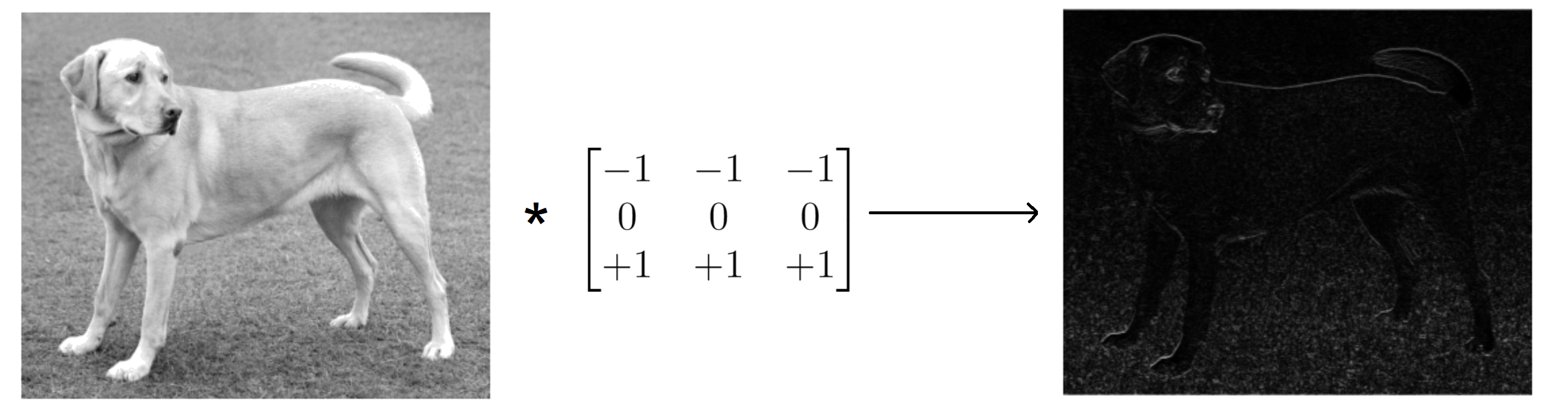
L’idée de l’architecture des modèles CNN est de garder des couches complètement connectées pour la classification. Cependant, en entrées de ces couches, l’image n’est pas directement utilisée, mais la sortie de plusieurs opérations de convolution qui ont pour but de mettre en avant les différentes caractéristiques d’une image en encodant d’une certaine façon les objets qui sont présents ou non. On utilise notamment des convolutions multi-canaux qui consistent à appliquer une convolution standard à chaque canaux de l’entrée puis sommer chaque produits de convolution obtenus pour obtenir une unique matrice 2D. Par exemple pour une image couleur les canaux sont le rouge, vert et bleu, on a alors 3 kernels à convoluer avec les canaux associés puis les 3 produits obtenus sont sommés.

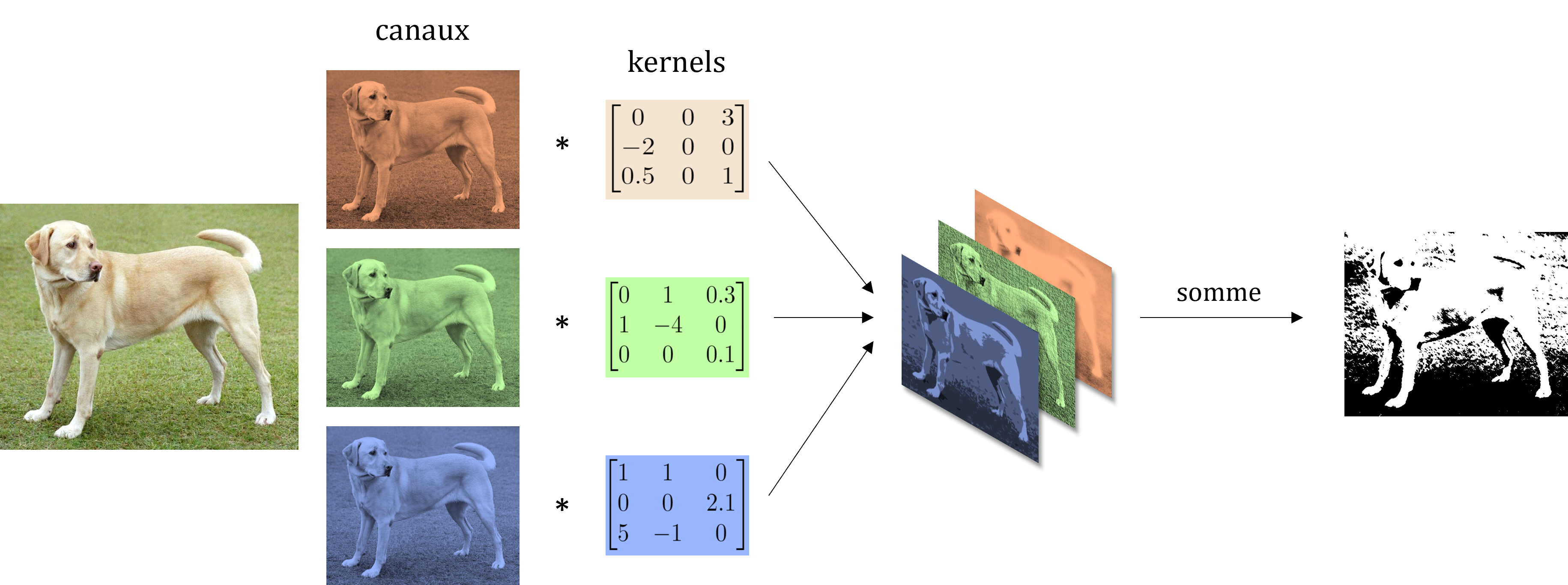
Note: En 2D (1 seul canal), on utilise le terme kernel pour parler du noyau. En 3D (plus d’un canal), on utilise le terme filtre qui est constitué d’autant de kernel que le nombre de canaux du volume d’entrée.

Plus précisément dans les CNN, une couche convolutionnelle est composée un ensemble de $N_f$ filtres de taille $N_W$ x $N_H$ x $N_C$ plus un biais par filtre suivi d’une fonction d’activation non linéaire. Ici, $N_W$ et $N_H$ désigne les tailles spatiales du filtre alors que $N_C$ est le nombre de canaux (parfois appelé feature map). Chaque filtres réalisent une convolution multi-canaux, on obtient alors $N_f$ produits de convolution qui sont concaténés dans un volume de sortie. Ces $N_f$ produits deviennent alors les canaux du prochain volume qui passera dans la prochaine couche convolutionnelle. Notez que la profondeur des filtres doit nécessairement correspondre au nombre de canaux du volume d’entrée de chaque couche mais le nombre de filtres est un hyperparamètre d’architecture du modèle. Au final, l’enchaînement de ces convolutions multicanaux crée en sortie un volume de caractéristiques (features) de l’image d’entrée, ces features sont alors passées au réseau complètement connecté pour la classification.

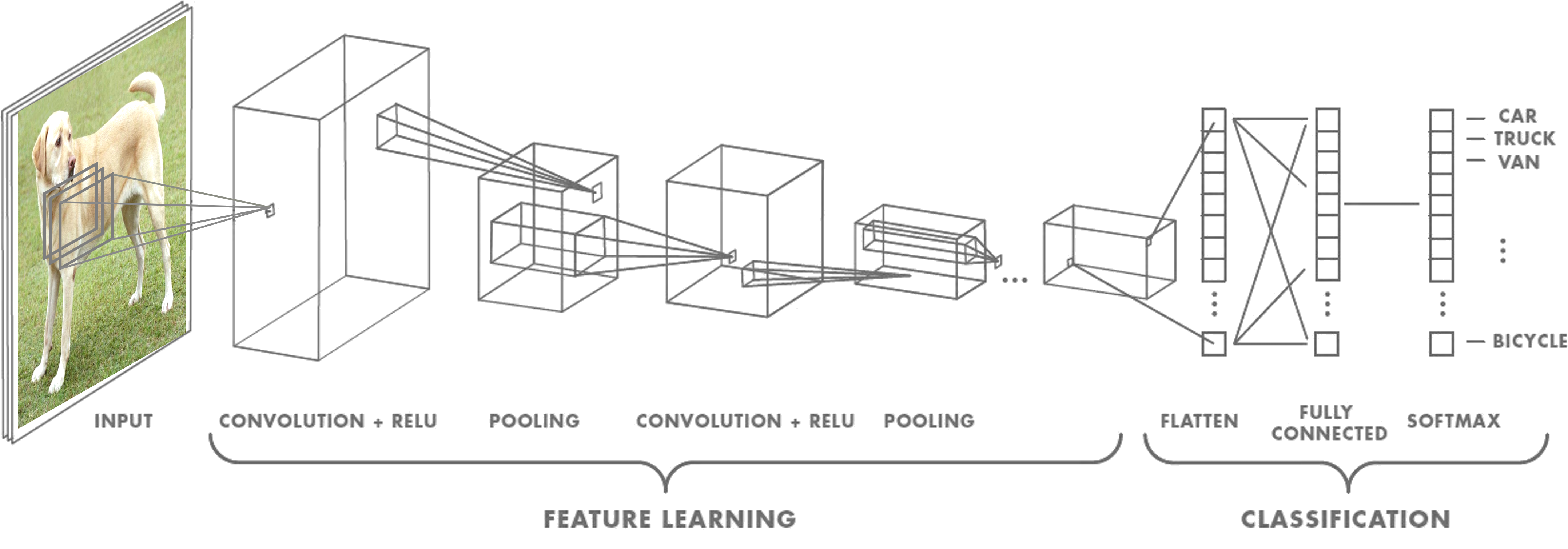
Important: Une couche convolutionnelle est généralement composée (en plus de la convolution) d’une fonction d’activation non linéaire et parfois d’autres types d’opérations (pooling, batch-normalization, dropout …).

Dans le post précédent, on a défini un MLP et son entraînement de zéro. Ici, la librairie PyTorch est utilisée. Elle permet de facilement construire des réseaux de neurones en profitant de son moteur de différentiation automatique pour l’entraînement ainsi que ses nombreuses fonctions spécialisées (comme la convolution).

import torch
import torch.nn as nn
import torch.nn.functional as F
from torch import optim

class My_Custom_Model(nn.Module):

    def __init__(self):
        ''' define some layers '''
        super().__init__()
        # feature learning
        self.conv1 = nn.Conv2d(3, 6, 5)
        self.pool  = nn.MaxPool2d(2, 2)
        self.conv2 = nn.Conv2d(6, 16, 5)
        # classification
        self.fc1 = nn.Linear(16*5* 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        ''' create model architecture - how operations are linked '''
        x = self.pool(F.relu(self.conv1(x)))
        x = self.pool(F.relu(self.conv2(x)))
        x = torch.flatten(x, 1)
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

Comme vous l’aurez peut être compris, ce qui est intéressant avec ces opérations de convolutions est que le poids des filtres peuvent être appris lors de l’optimisation par rétropropogation du gradient puisqu’il est possible de calculer de façon exacte la valeur de $\frac{\partial\mathcal{L}}{\partial W}$ par dérivation en chaîne.

# define loss and optimizer
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(my_cnn_model.parameters(), lr=0.001)
# training loop
num_epochs = 100
for epoch in range(num_epochs):
    for i, data in enumerate(train_loader):
        images, labels = data
        # Forward pass
        outputs = model(images)
        loss = criterion(outputs, labels)
        # Backward pass
        optimizer.zero_grad()
        loss.backward()
        # optimization step
        optimizer.step()

Note: Pour des données d’entrées volumineuses, on utilise souvent comme algorithme d’optimisation une descente de gradient stochastique où la loss est approchée en utilisant un batch de quelques données (par exemple, 8, 16 ou 32 images).

Deep Dream

L’un des challenges des réseaux de neurones est de comprendre ce qu’il se passe exactement à chaque couche. En effet, leur architecture en cascade ainsi que leurs nombreuses interconnexions font qu’il n’est pas évident d’interpréter le rôle de chaque filtre. La visualisation des features est un axe de recherches s’étant développé ces dernières années qui consiste à trouver des méthodes pour comprendre comment les CNNs voient un image.

DeepDream est le nom d’une de ces techniques créée en 2015 par une équipe d’ingénieur de Google, l’idée est d’utiliser un réseau déjà entraîné à reconnaître des formes pour modifier une image afin qu’un neurone donné renvoie une sortie plus élevée que les autres. L’algorithme ressemble à la backpropagation classique mais au lieu de modifier les poids du réseau on ajuste les pixels de l’image d’entrée. De plus, le critère d’optimisation n’est pas une cross entropie mais directement la norme de la sortie du neurone à visualiser (ça peut être la couche entière ou un filtre) qu’on va chercher à maximiser, on fait alors une montée de gradient (on pourrait également minimiser l’opposée).

# Parameters
iterations   = 25   # number of gradient ascent steps per octave
at_layer     = 26   # layer at which we modify image to maximize outputs
lr           = 0.02 # learning rate
octave_scale = 2    # image scale between octaves
num_octaves  = 4    # number of octaves

# Load Model pretrained
network = models.vgg19(pretrained=True)
# Use only needed layers
layers = list(network.features.children())
model = nn.Sequential(*layers[: (at_layer + 1)])
# Use GPU is available
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
model = model.to(device)

Une astuce supplémentaire pour obtenir une visualisation intéressante est d’opérer à des résolutions spatiales différentes, ici on parle d’octave. De plus, la loss est normalisée à toutes les couches pour que la contribution des grandes couches ne l’emporte pas sur celle des petites couches.

# loop on different resolution scale
detail = np.zeros_like(octaves[-1])
for k, octave_base in enumerate(tqdm(octaves[::-1], desc="Octaves : ")):
    # Upsample detail to new octave dimension
    if k > 0: 
      detail = nd.zoom(detail, np.array(octave_base.shape)/np.array(detail.shape), order=1) 
    # Add detail from previous octave to new base
    input_image = octave_base + detail
    # Updates the image to maximize outputs for n iterations
    input_image = Variable(torch.FloatTensor(input_image).to(device), requires_grad=True)
    for i in trange(iterations, desc="Iterations : ", leave=False):
        model.zero_grad()
        out  = model(input_image)
        loss = out.norm()
        loss.backward()
        # gradient ascent
        avg_grad = np.abs(input_image.grad.data.cpu().numpy()).mean()
        norm_lr  = lr/avg_grad
        input_image.data = input_image.data + norm_lr * input_image.grad.data
        input_image.data = clip(input_image.data)
        input_image.grad.data.zero_()
        # Extract deep dream details
        detail = input_image.cpu().data.numpy() - octave_base

On obtient, selon le nombre d’itération, des images de plus en plus abstraites avec des formes psychédéliques qui apparaissent au fur et à mesure d’où le nom de DeepDream. En fait, ces formes abstraites sont présentes surtout pour les couches les plus profondes, les premières couches accentuent généralement des features simples comme des arêtes, des coins, des textures …

Avec cet outil, on peut créer des effets artistiques très avancées comme sur l’instagram de DeepDreamGenerator. Mais on peut également accentuer l’effet pscychédélique en faisant beaucoup d’itérations ou en alimentant plusieurs fois la sortie de l’algorithme en entrée. Et avec un peu d’effort, on peut parvenir à visualiser à quoi ça ressemble d’aller au supermarché dans ces rêves à partir d’images bien réelles.

Tel que présenté ci-dessus, Deep Dream présente un inconvénient si on veut le lancer sur une image de bruit blanc en entrée pour visualiser ce qui pourrait en émerger et ainsi avoir une représentation plus exact des features du CNN. En effet, on voit que l’image reste dominée par des motifs hautes-fréquences.

Généralement, pour contrer cet effet, ce qui marche le mieux est d’introduire une régularisation d’une façon ou d’une autre dans le modèle. Par exemple, la robustesse à la transformation essaie de trouver des exemples qui activent toujours fortement la fonction d’optimisation lorsqu’on les transforment très faiblement. Concrètement, cela signifie qu’on tremble, tourne, diminue ou augmente l’image de façon aléatoire avant d’appliquer l’étape d’optimisation. Les librairies lucid (tensorflow) et lucent (pytorch) sont des packages open-source qui implémentent toutes sortes de méthodes de visualisation.

# load librairies
from lucent.optvis import render
from lucent.modelzoo import vgg19
# load model
model = vgg19(pretrained=True)
model = model.to(device)
model.eval()
# run optimisation
image = render.render_vis(model, "features:30",thresholds=[100],show_inline=True)