Kalman : filtre, tracking, IMU
Le filtre de Kalman est une méthode très répandue dans le milieu de l’ingénieurie puisqu’elle posséde de nombreuses applications en localisation, navigation, pilotage automatique, suivi d’objet, fusion de données … Il fut introduit en 1960 par l’ingénieur Rudolf E. Kálmán et fut notamment utilisé pour l’estimation de trajectoire pour le programme Apollo. En effet, à partir d’une série de mesures observées au cours du temps (bruitée et biaisée), il permet de calculer une estimation de ces variables inconnues souvent plus précise que les mesures en se basant sur les théories du contrôle et des statistiques. L’une des forces de ce filtre est sa capacité à s’améliorer au cours du temps en intégrant un terme d’erreur du modèle lui-même. Il a de nombreux autres avantages : fusionner les mesures de capteurs différents, fonctionner en ligne, facile à implémenter …

Principe
La construction du filtre de Kalman part de 3 hypothèses importantes :
- le système modélisé est linéaire : il peut être modélisé comme une multiplication entre l’état $t$ et $t-1$.
- le bruit des mesures est blanc : il est non corrélé avec le temps.
- le bruit est gaussien : il est décrit par une moyenne et une covariance
L’idée consiste à construire un modèle pour l’état du système qui maximise la probabilité a posteriori de ces mesures précédentes. Cela signifie que le nouveau modèle que nous construisons après avoir effectué une mesure (en tenant compte à la fois de notre modèle précédent avec son incertitude et de la nouvelle mesure avec son incertitude) est le modèle qui a la plus forte probabilité d’être correct. De plus, on peut maximiser la probabilité a posteriori sans conserver un long historique des mesures précédentes elles-mêmes. Au lieu de cela, on met à jour de manière itérative le modèle de l’état du système et on ne garde que ce modèle pour la prochaine itération. Cela simplifie grandement l’implication de calcul de cette méthode.
Cas unidimensionnel statique
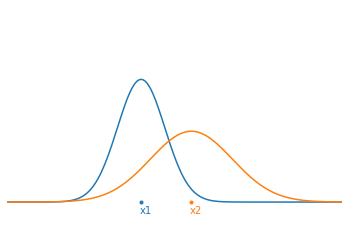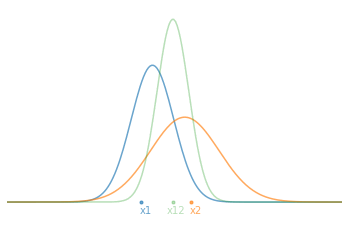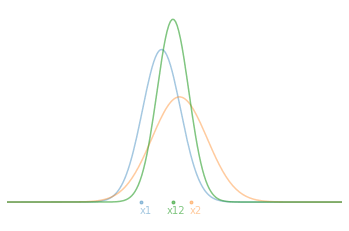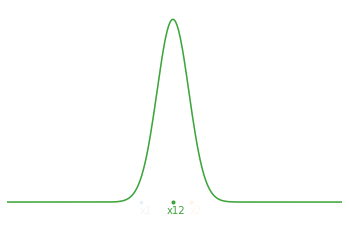
Supposons qu’on veuille savoir où est positionner un point fixe sur une ligne et qu’on ait 2 mesures bruitées $x_1$ et $x_2$. Chacune de ces mesures suit une distribution gaussienne :
\[p_i(x) = \frac{1}{\sigma_i\sqrt{2\pi}} e^{-\frac{(x-\bar{x}_i)^2}{2\sigma_i^2} } \quad (i=1,2)\]On peut alors montrer que la combinaison de ces 2 mesures gaussiennes est équivalente à une seule mesure gaussienne caractérisée par la moyenne $\bar{x}_{12}$ et la variance $\sigma_{12}^2$ :
\[\begin{aligned} \bar{x}_{12} &= \left( \frac{\sigma_2^2}{\sigma_1^2+\sigma_2^2} \right)x_1 + \left( \frac{ \sigma_1^2}{\sigma_1^2+\sigma_2^2} \right)x_2 \\ \\ \sigma_{12}^2 &= \frac{\sigma_1^2\sigma_2^2}{\sigma_1^2+\sigma_2^2} \end{aligned}\]Ainsi, la nouvelle valeur moyenne $\bar{x}_{12}$ n’est qu’une combinaison pondérée des deux mesures par les incertitudes relatives. Par exemple, si l’incertitude $\sigma_2$ est particulièrement plus grande que $\sigma_1$, alors la nouvelle moyenne sera très proche de $x_1$ qui est plus certaine.
Maintenant, si on part du principe que l’on effectue nos 2 mesures l’une après l’autre et qu’on cherche donc à estimer l’état courant de notre système $(\hat{x}_t,\hat{\sigma}_t)$. Au temps $t=1$, on a notre première mesure $\hat{x}_1=x_1$ et son incertitude $\hat{\sigma}_1^2=\sigma_1^2$. En substituant ceci dans nos équations d’estimation optimales et en les réarrangeant pour séparer l’ancienne informations de la nouvelle, on obtient :
\[\begin{aligned} \hat{x}_2 &= \hat{x}_1 + \frac{\hat\sigma_1^2}{\hat{\sigma_1^2}+\sigma_2^2}(x_2 - \hat x_1 ) \\ \\ \hat \sigma_2^2 &= \left( 1 - \frac{\hat \sigma_1^2}{\hat\sigma_1^2+\sigma_2^2} \right) \hat \sigma_1^2 \end{aligned}\]En pratique, on appelle couramment le terme $x_2 - \hat x_1$ l’innovation et on note le facteur $K = \frac{\hat \sigma_1^2}{\hat \sigma_1^2+\sigma_2^2}$ le gain de mise à jour. Au final, on peut écrire la relation de récurrence au temps $t$ :
\[\begin{aligned} \hat x_t &= \hat x_{t-1} + K (x_t - \hat x_{t-1}) \\ \\ \hat \sigma_t^2 &= (1 - K) \hat \sigma_{t-1}^2 \end{aligned}\]Attention : Dans la littérature, on voit plus souvent l’indice $k$ pour décrire le pas de temps (ici noté $t$).
Si on regarde la formule et à la valeur du gain de Kalman $K$, on comprend que si le bruit de mesure est élevé ($\sigma^2$ élevé) alors $K$ sera proche de $0$ et l’influence de la nouvelle mesure $x_t$ sera faible. Au contraire, si $\sigma^2$ est petit, l’état du système $\hat x_t$ sera ajusté fortement vers l’état de la nouvelle mesure.
Cas unidimensionnel dynamique
On a considéré précemment le cas d’un système statique dans un état $x$ ainsi qu’une série de mesures de ce système. Dans un cas dynamique où l’état du système varie au cours du temps, on divise l’estimation du filtre de Kalman en 2 étapes :
- la phase de prédiction : on utilise les informations passées et le modèle dynamique pour prédire l’état prochain du système. On prédit également la covariance de l’erreur. Elle modélise l’état du système.
- la phase de correction ou mise à jour : on combine la prédiction faite avec une nouvelle mesure pour affiner le modèle et l’estimation de l’état du système ainsi que la covariance de l’erreur. Elle modélise la mesure du système.
Par exemple, si on mesure la position d’une voiture au temps $t-1$ puis au temps $t$. Si la voiture a une vitesse $v$ alors on n’intègre pas directement la nouvelle mesure directement. D’abord, on fast-forward notre modèle basé sur ce qu’on savait au temps $t-1$ pour avoir une prédiction de l’état au temps $t$. De cette manière, la nouvelle mesure acquise au temps $t$ est fusionnée non pas avec l’ancien modèle du système mais avec l’ancien modèle du système projeté vers l’avant au temps $t$
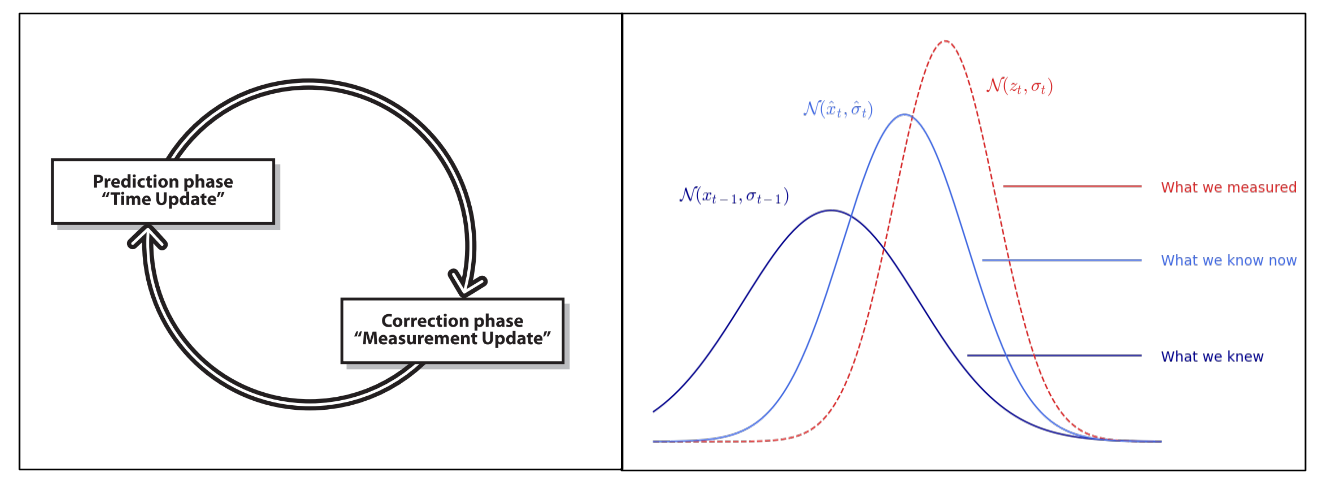
En partant de l’hypothèse que la dynamique du système modélisé est linéaire, la phase de prédiction s’écrit alors :
\[\left. \begin{aligned} \hat x_t &= a \ \hat x_{t-1} \\ \hat \sigma_t^2 &= a^2 \ \hat \sigma_{t-1}^2 \\ &\scriptsize \color{blue} \text{car $var(ax+b) = a^2 var(x)$} \end{aligned} \right.\]Et la phase de correction calculée dans la section précédente :
\[\left. \begin{aligned} \hat x_t &= \hat x_{t-1} + K (z_t - \hat x_{t-1}) \\ \hat \sigma_t^2 &= (1 - K) \hat \sigma_{t-1}^2 \\ \end{aligned} \right.\]
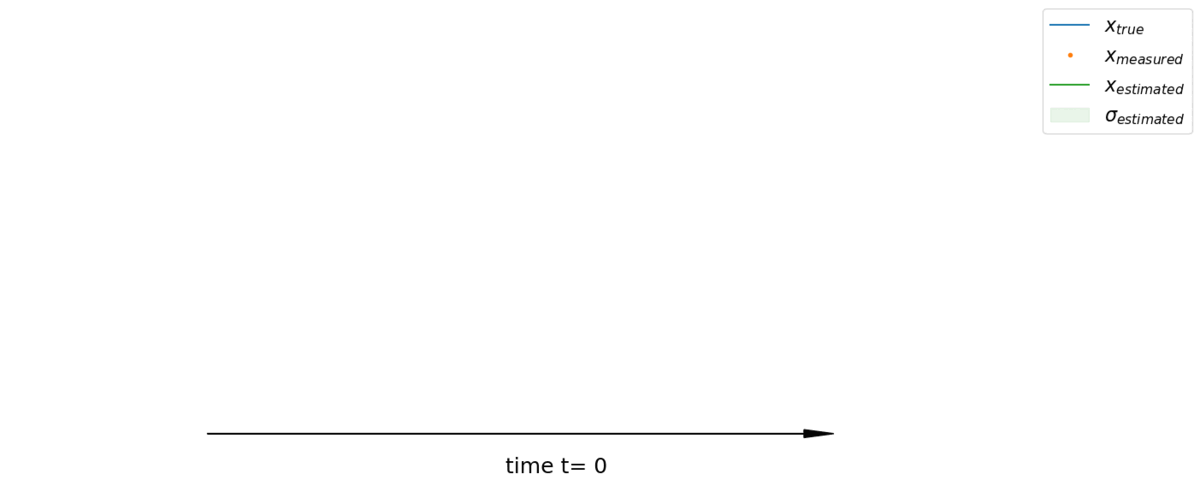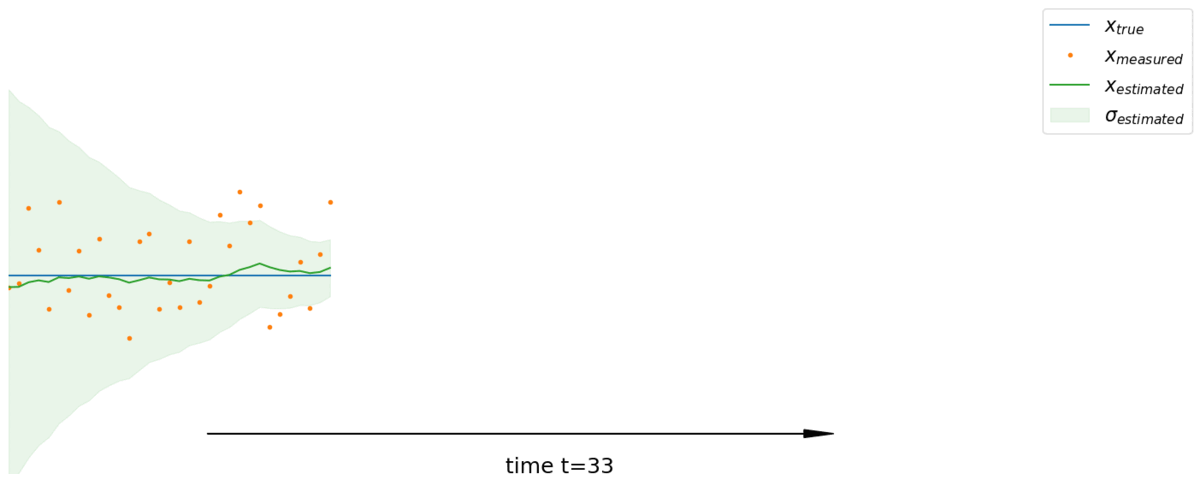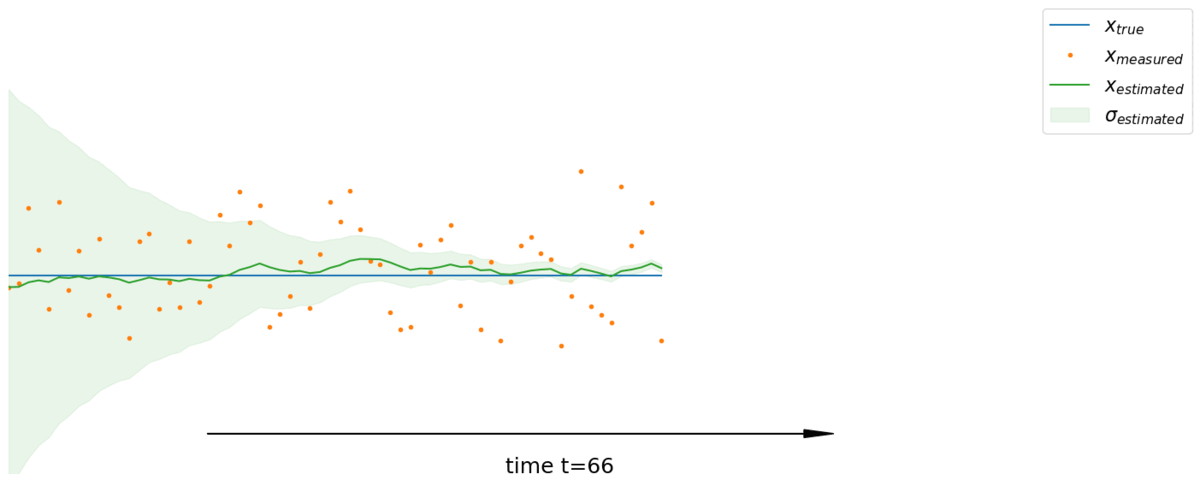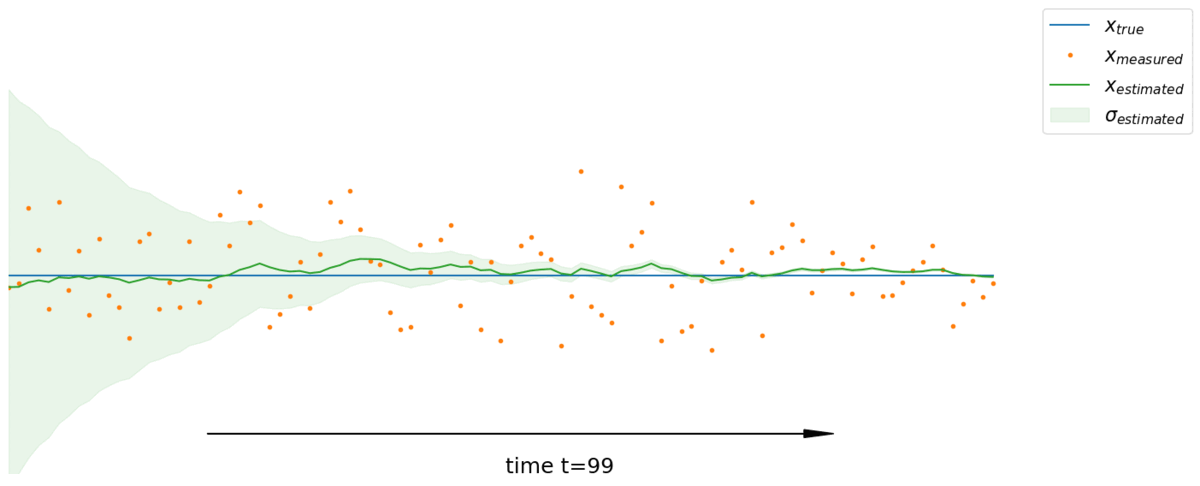
Généralisation
On peut étendre les équations précédentes au cas multidimensionnel où l’état de notre système est défini par plusieurs grandeurs. On cherche alors à estimer l’état du système $\hat X \in \mathbb{R}^d$ à l’instant $t$ ainsi que sa matrice de covariance associée $\hat P \in \mathbb{R}^{d \times d}$ (avec $d$ la dimension du système). Les équations deviennent :
phase de prédiction
\[\left. \begin{aligned} \hat X_t &= A \hat X_{t-1} \\ \hat P_t &= A P_{t-1} A^T + Q \end{aligned} \right.\]où $A \in \mathbb{R}^{d \times d}$ est la matrice de transition d’état modélisant la dynamique du système et $Q \in \mathbb{R}^{d \times d}$ la matrice de covariance du bruit de processus capturant les erreurs non modélisées par $A$ (plus elle est grande, plus on fait confiance aux mesures plutôt qu’aux prédictions du modèle dynamique).
phase de correction
\[\left. \begin{aligned} \hat X_t &= \hat X_t + K(Z_t - \hat X_t) \\ \hat P_t &= \hat P_t - K \hat P_t \end{aligned} \right.\]avec le gain de Kalman $ K = \hat P_t (\hat P_t + R)^{-1} $
où $Z \in \mathbb{R}^d$ est la mesure du système (ou observation) et $R \in \mathbb{R}^{d \times d}$ la matrice de covariance de la mesure qui modélise l’erreur des mesures.
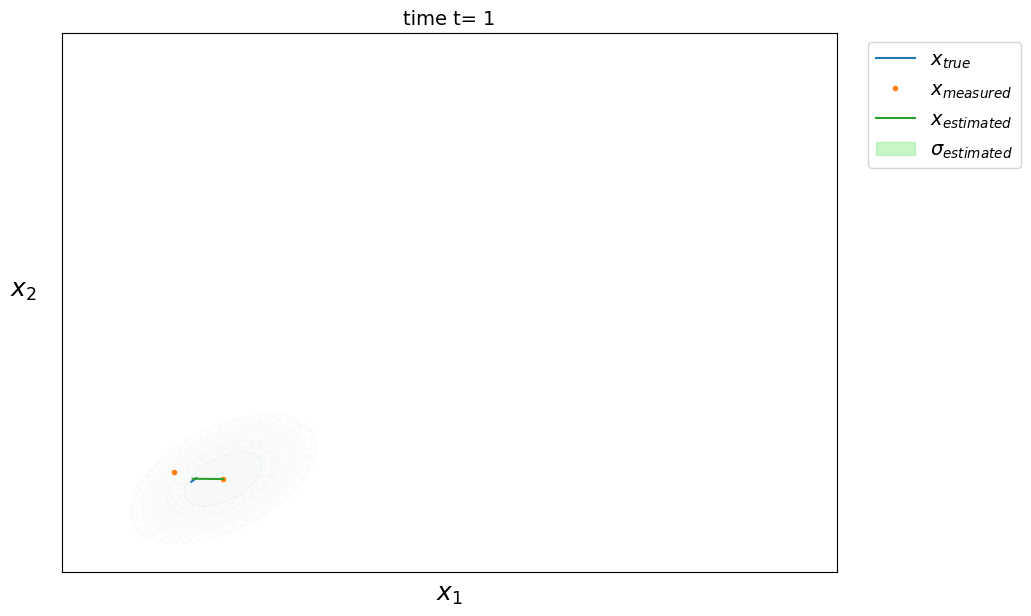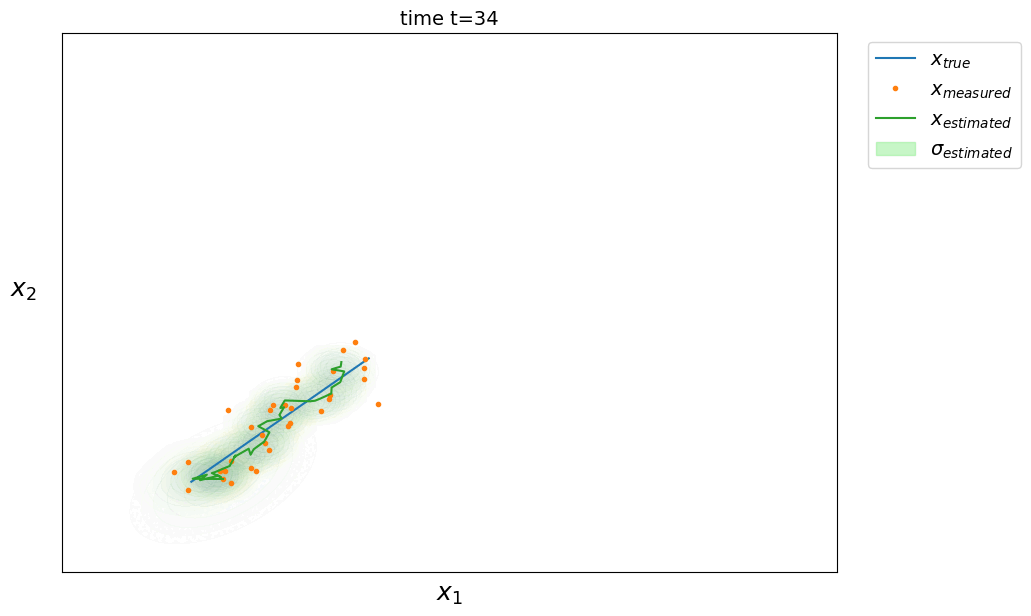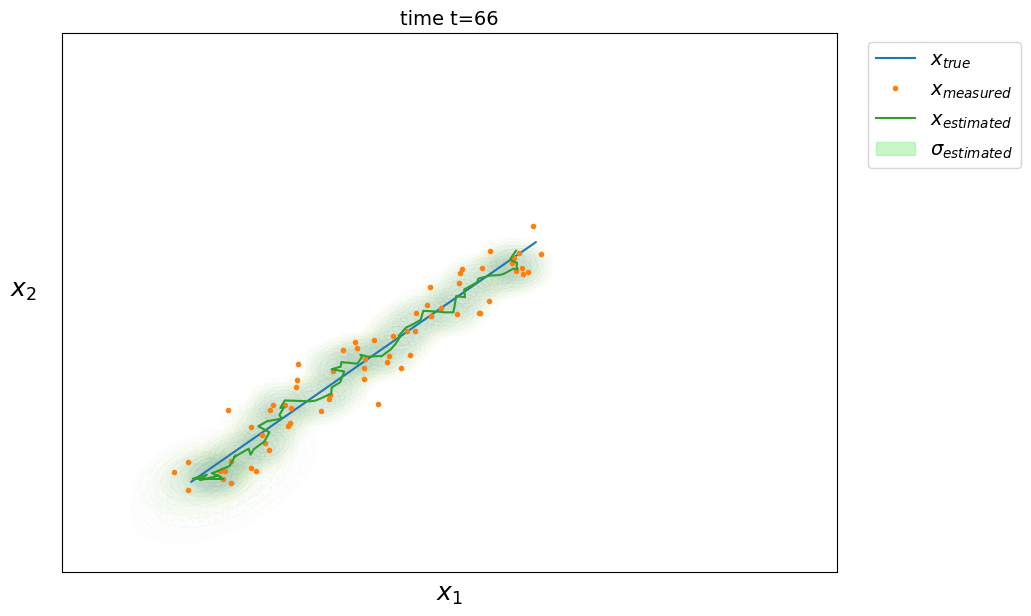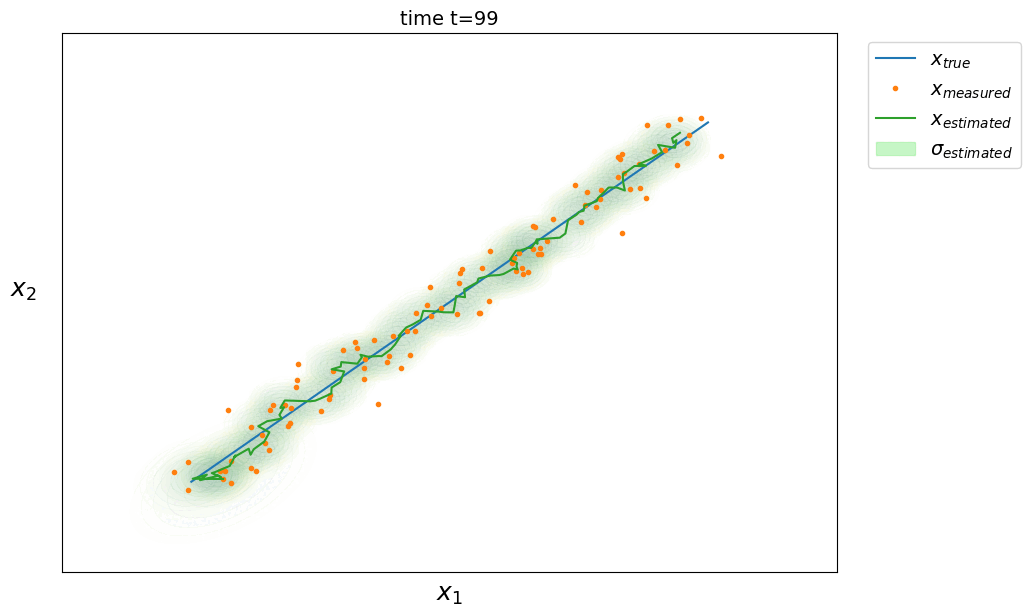
Il existe des versions plus élaborées du filtre de Kalman qui peuvent prendre en entrée une commande $U$ envoyée au système. On trouve également fréquemment la matrice d’observation $H \in \mathbb{R}^{d \times m}$ reliant l’état réel du système au variables observées, en effet on peut modéliser un système à $d$ dimensions mais seulement observer $m$ de ses variables ($m<d$). La phase de prédiction reste la même mais la phase de correction est alors :
\[\begin{aligned} \hat X_t &= \hat X_t + K(\textcolor{blue}{H} Z_t - \hat X_t) \\ \hat P_t &= \hat P_t - K \textcolor{blue}{H} \hat P_t \end{aligned}\]avec le gain de Kalman $ K = \hat P_t \textcolor{blue}{H^t} (\textcolor{blue}{H} \hat P_t \textcolor{blue}{H^T} + R)^{-1} $
Exemples
Le filtre de Kalman est un outil générique et ces équations peuvent facilement s’implémenter en quelques lignes :
def kalman_estimation(X_est, P_est, Z_obs):
# state prediction
X_est = A @ X_est
P_est = A @ P_est @ A.T + Q
# observation
Z_pred = H @ X_est
# kalman gain
K = P_est @ H.T @ np.linalg.inv(H @ P_est @ H.T + R)
# correction phase
if Z_obs:
X_est = X_est + K @ (Z_obs - Z_pred)
P_est = P_est - K @ H @ P_est
# return final estimation
return X_est, P_est
Note: Si l’observation n’est pas disponible à l’instant $t$, on execute seulement la phase de prédiction du filtre de Kalman pour avoir une estimation grâce au modèle dynamique.
Cependant, la partie cruciale du problème réside la plupart du temps dans la définition des paramètres du système $A$, $Q$, $H$ et $R$ afin que le filtre fonctionne correctement. De plus, il peut devenir puissant lorsqu’il permet d’estimer une grandeur qui n’est pas mesurée comme dans les exemples ci-dessous avec la vitesse d’un objet et le biais d’un gyroscope.
Suivi d’objet (Tracking)
On veut implémenter un filtre de Kalman appliqué à un problème de suivi d’objet sur une image. L’objet est repéré par un détecteur d’objet basique en regardant un intervalle de couleur dans l’espace HSV qui retourne la position $(x,y) \in \mathbb{N}^2$ en pixel dans l’image.
def simple_detector(image):
# go to HSV space
image = cv2.cvtColor(image, cv2.COLOR_BGR2HSV)
# look into interval
mask = cv2.inRange(image, np.array([155, 50, 50]) , np.array([170, 255, 255]))
# sort by contour
obj = cv2.findContours(mask, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)[-2]
obj = sorted(obj, key=lambda x:cv2.contourArea(x), reverse=True)
# keep center point
if obj:
(cX, cY), _ = cv2.minEnclosingCircle(obj[0])
Z = [cX, cY]
# return empty if no detection
else:
Z = []
return Z
À chaque instant $t$, les déplacements de l’objet sont modélisés par l’équation de mouvement suivante :
\[x_{t+1} = x_t + \Delta t \ \dot x_t\]où $\Delta t \in \mathbb{R}$ est le pas de temps, $x_t$ la position et $\dot x_t$ la vitesse de l’objet à $t$. L’état du système est décrit par la position et la vitesse en 2 dimensions : $ X_t = \begin{bmatrix} x_t & y_t & \dot x_t & \dot y_t \end{bmatrix}^T $. Pour obtenir la matrice de transition d’état $A$, on écrit la dynamique du système sous forme matricielle :
\[\begin{array}{cc} &\Rightarrow& \left\{ \begin{array}{cc} x_{t+1} &=& x_t &+& 0 y_t &+& \Delta t \ \dot x_t &+& 0 \dot y_t \\ y_{t+1} &=& 0 x_t &+& y_t &+& 0 \dot x_t &+& \Delta t \ \dot y_t \\ \dot x_{t+1} &=& 0 x_t &+& 0 y_t &+& \dot x_t &+& 0 \dot y_t \\ \dot y_{t+1} &=& 0 x_t &+& 0 y_t &+& 0 \dot x_t &+& 1 \dot y_t \end{array} \right. \\ \\ \\ &\Rightarrow& \begin{array}{cc} X_{t+1} &=& \underbrace{ \begin{bmatrix} 1 & 0 & \Delta t & 0 \\ 0 & 1 & 0 & \Delta t \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}}_A X_t \end{array} \end{array}\]De plus, le détecteur permet d’obtenir seulement la position $(x,y)$ mais pas la vitesse $(\dot x, \dot y)$, la matrice d’observation est donc $H = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{bmatrix} $ pour relier seulement les 2 premières variables du système à notre observation. Les paramètres $Q$ et $R$ peuvent être affiner également en fonction du bruit de notre détecteur et du modèle. En python, on a :
# Initial state
X = np.array([500, 500, 0, 0]) # can be adjusted with 1st observation
P = np.eye(4)
# Kalman parameters
dt = 0.1
A = np.array([[1, 0, dt, 0], [0, 1, 0, dt], [0, 0, 1, 0], [0, 0, 0, 1]])
H = np.array([[1, 0, 0, 0], [0, 1, 0, 0]])
Q = np.eye(4)
R = np.eye(2)
On ouvre la vidéo et pour chaque frame, on détecte la position de l’objet puis on applique le filtre de Kalman. Il nous permet d’avoir accès à la vitesse du système qui n’est pas observé. La vitesse est représentée dans l’exemple ci-dessous par la flèche. De plus, si la détection échoue et que la position de l’objet n’est pas disponible à l’instant $t$, on exécute seulement la phase de prédiction du filtre de Kalman pour avoir malgré tout une estimation grâce au modèle dynamique.
# open video
cap = cv2.VideoCapture(r'path\to\my\video.mp4')
# loop on video frame
while True:
# get frame
ret, frame = cap.read()
if not ret:
break
# simple object detection
Z_obs = simple_detector(frame)
# kalman filter
X, P = kalman_estimation(X, P, Z_obs)
# displaying
plt.imshow(cv2.cvtColor(frame, cv2.COLOR_BGR2RGB))
plt.plot(Z_obs[0], Z_obs[1], 'r.', label="detected")
plt.plot(X[0], X[1], 'g.', label="kalman")
plt.arrow(X[0], X[1], X[2], X[3], color='g', head_length=1.5)
plt.legend(loc="upper right")
plt.axis("off")
# close video
cap.release()
Central inertiel (IMU)
Les Inertial Measurement Unit sont des capteurs électroniques qu’on trouve de nos jours un peu partout (téléphones, drones, avion, nintendo wii …), ils permettent de mesurer l’accélération et la vitesse angulaire d’un objet pour ensuite estimer l’orientation et la position par intégration. L’accélération est mesurée par un accéléromètre et la vitesse angulaire par un gyroscope mais la difficulté vient du fait que le gyroscope possède un biais évoluant avec le temps. Si on ne corrige pas cette dérive, on aura l’impression que l’objet s’incline lentement alors qu’en réalité, celui-ci ne bouge pas !

La dynamique du système se modélise comme dans l’exemple précédent avec l’équation de mouvement angulaire :
\[\alpha_{t+1} = \alpha_t + \Delta t \ \dot \alpha_t\]où $\Delta t \in \mathbb{R}$ est le pas de temps, $\alpha_t$ l’angle et $\dot \alpha_t$ la vitesse angulaire. L’état du système est, au final, décrit par l’angle, la vitesse angulaire et le biais $b$ (qu’on n’observe pas) : $X_t = \begin{bmatrix} \alpha_t & \dot \alpha_t & b_t \end{bmatrix}^T$. Ne connaissant pas le modèle d’évolution du biais $b$ du gyroscope, on le considére fixe ici. On a alors sous forme matricielle :
\[X_{t+1} = \underbrace{\begin{bmatrix} 1 & \Delta t & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}}_A X_t\]Remarque: On modélise ici un cas simpliste où l’accéléromètre nous donne directement $\alpha$, l’angle d’inclinaison par rapport à la force de gravitation (qui n’est rien d’autre qu’une accélération !), l’objet tourne mais ne se déplace pas. En l’orientant vers le sol (selon l’axe Z), on obtient une accélération de 9.8 m/s², la constante $g$. Pour obtenir une mesure de l’angle d’orientation, il suffit donc de prendre $-\arcsin(a_{mesure}/g)$.
Comme énoncé précédemment, le biais $b$ n’est pas une grandeur observée par notre IMU. La matrice d’observation apparait clairement en écrivant la relation reliant l’observation biaisé de la vitesse angulaire $\dot \alpha_{observé} = \dot \alpha_{vraie} + b$. C’est-à-dire :
\[\underbrace{\begin{bmatrix} \alpha \\ \dot \alpha + b \end{bmatrix}}_{observation} = \underbrace{\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 1 \end{bmatrix}}_H \quad \underbrace{\begin{bmatrix} \alpha \\ \dot{\alpha} \\ b \end{bmatrix}}_X\]Enfin, il faut déterminer comment remplir $R$, le bruit de mesure et $Q$, le bruit du modèle. La matrice $R$ est simplement composé du bruit des capteurs sur la diagonale (pas de covariance car capteurs décorrélés entre eux) soit $R = \begin{bmatrix} \sigma_1^2 & 0 \\ 0 & \sigma_2^2\end{bmatrix}$. La matrice $Q$ représente les erreurs de modélisation de $A$ : par exemple on a modélisé que le biais $b$ et que la vitesse angulaire $\dot \alpha$ étaient constants, ce qui est faux, on mettra des termes assez élevés à ces endroits et on les affinera empiriquement en fonction des données du problème. Par contre, l’erreur du modèle sur l’angle $\alpha$ peut être fixée à $0$ puisque l’équation d’état détermine parfaitement sa valeur en fonction de $\dot \alpha$. Ici, on a $Q = \begin{bmatrix} 0 & 0 & 0 \\ 0 & \epsilon_{\dot \alpha} & 0 \\ 0 & 0 & \epsilon_b\end{bmatrix} = \scriptsize \textcolor{blue}{\begin{bmatrix}0 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 5 \end{bmatrix} \leftarrow \textit{déterminé empiriquement}}$
En python, je commence par générer synthétiquement les données du problèmes. L’angle est une fonction sinusoïdale avec un biais qui évolue au cours du temps et la vitesse angulaire est sa dérivée, on ajoute un bruit gaussien à ces données pour avoir notre vecteur d’observation, la mesure qui sort des capteurs.
dt = 0.05 # time step
T = 10 # total time
N = int(T/dt) # number of data
times = np.arange(0, T, dt) # time array
# Define state vector to be estimated (normally unknown)
X_true = np.zeros((N, 3))
X_true[:, 0] = -1 * np.pi * np.cos(np.pi * times) + np.pi
X_true[:, 1] = np.diff(X_true[:,0], prepend=-np.pi*dt)/dt # velocity as derivative of position
X_true[:, 2] = 10 * times + 20 * np.sin(2 * np.pi * 0.1 * times)
# Noise sensors
noise = np.zeros((N,2))
s = np.array([np.pi**2 * 0.06, np.pi * 0.2])
noise[:,0] = s[0] * np.random.randn(N)
noise[:,1] = s[1] * np.random.randn(N)
# Generate observation
X_obs = np.zeros((N, 2))
X_obs[:, 0] = X_true[:, 0] + noise[:,0]
X_obs[:, 1] = X_true[:, 1] + X_true[:, 2] + noise[:,1]
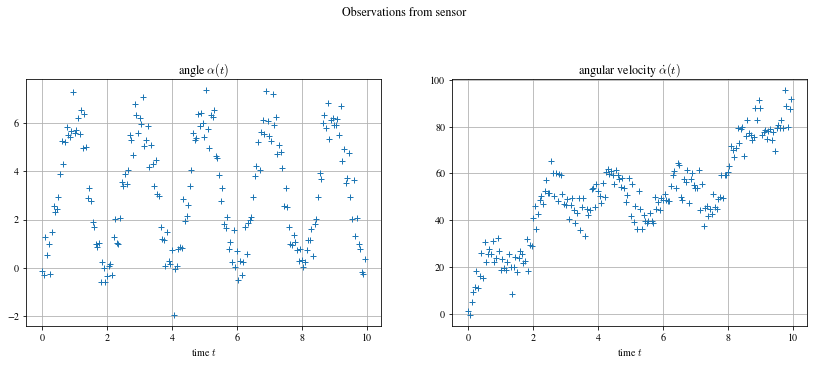
On peut ensuite déclarer les paramètres de Kalman définis précédement et initialiser le variable d’état et sa covariance estimés par le filtre (ici, X_est et P_est). De plus, je sauvegarde l’historique des valeurs dans X_kalman.
# Kalman filter parameter
H = np.array([[1,0,0],[0,1,1]])
R = np.array([[s[0]**2,0],[0,s[1]**2]])
A = np.array([[1,dt,0],[0,1,0],[0,0,1]])
Q = np.array([[0,0,0],[0,3,0],[0,0,5]])
# initial state
X_est = np.zeros(3)
P_est = np.zeros((3,3))
X_kalman = np.zeros((N, 3))
# loop over time
for t in range(2,N):
X_est, P_est = kalman_estimation(X_est, P_est, X_obs[t, :].T)
# save history
X_kalman[t, :] = X_est
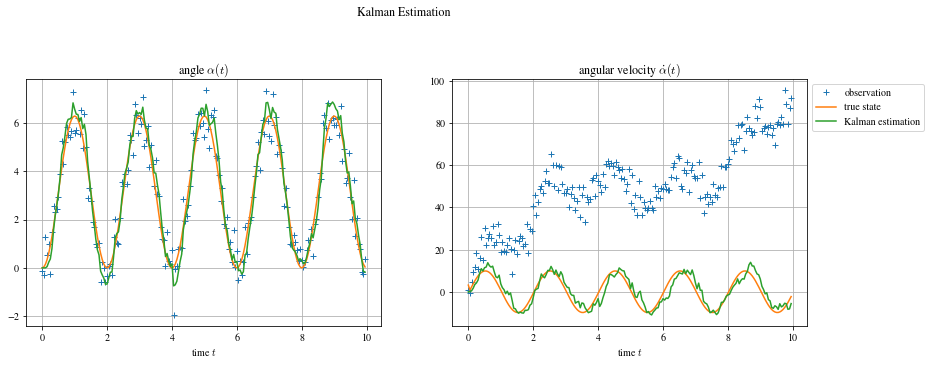
Ayant généré synthétiquement les données, l’état réel du système est disponible (ce qui n’est pas le cas en pratique). On peut donc comparer l’erreur du filtre à l’erreur si on prenait directement la mesure, on calcule les résidus $RSS = \sum_i^N (y_i - \hat y_i)^2$ et on a, pour le filtre de kalman, $RSS_{kalman} = [38; 2007]$ et, sans filtre, $RSS_{observation} = [80; 575873]$. La différence est flagrante pour la 2e variable $\dot \alpha$ où le biais est pris en compte par Kalman.
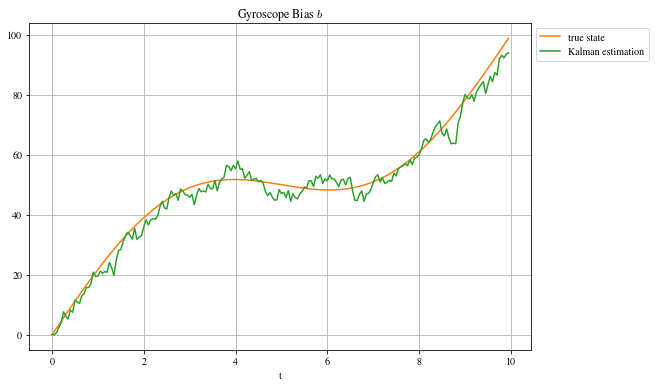
Pour aller plus loin
Une limite importante du filtre présenté ici est qu’il modélise une dépendance linéaire avec le temps ce qui est assez rare en pratique. On peut malgré tout l’utiliser et obtenir de bon résultat comme montré dans les exemples ci-dessus mais il existe une version non linéaire appelé filtre de Kalman étendu où $A$ est remplacé par une fonction $f$ non linéaire et différentiable dans l’équation de prédiction d’état et sa jacobienne $F=\frac{\partial f}{\partial x}$ dans l’équation de prédiction de la covariance. Cette solution est généralement utilisée dans les système de navigation et les GPS mais on note qu’elle peut parfois être instable (divergence) selon l’initialisation de l’état initial contrairement à la version linéaire.
Un autre avantage du filtre de Kalman est d’être capable de faire de la fusion de capteurs. Un exemple très simple serait d’avoir un système où l’on a accès à 2 capteurs bruités mesurant la même grandeur, par exemple pour un radar et un GPS qui mesurent la position $x$ on aurait alors la matrice d’observation $H$ via $\begin{bmatrix} x_{radar} \\ x_{GPS} \end{bmatrix} = \underbrace{\begin{bmatrix} 1 & 0 \\ 1 & 0 \end{bmatrix}}_H \begin{bmatrix} x \\ \dot x \end{bmatrix}$, et on profiterait ainsi des 2 informations des 2 capteurs différents dans nos prédictions.






Laisser un commentaire