Réduction de Dimension : PCA, t-SNE et UMAP

10 minute(s) de lecture

Dans le monde de la data science, nous sommes souvent confrontés à des jeux de données possédant un grand nombre de caractéristiques (features). Si cette richesse d’information peut être bénéfique, elle apporte aussi son lot de défis, connus sous le nom de “fléau de la dimensionnalité” (curse of dimensionality). Plus le nombre de dimensions augmente, plus l’espace des données devient vaste et épars, rendant l’analyse, la visualisation et même l’entraînement de modèles de machine learning complexes et coûteux en ressources.

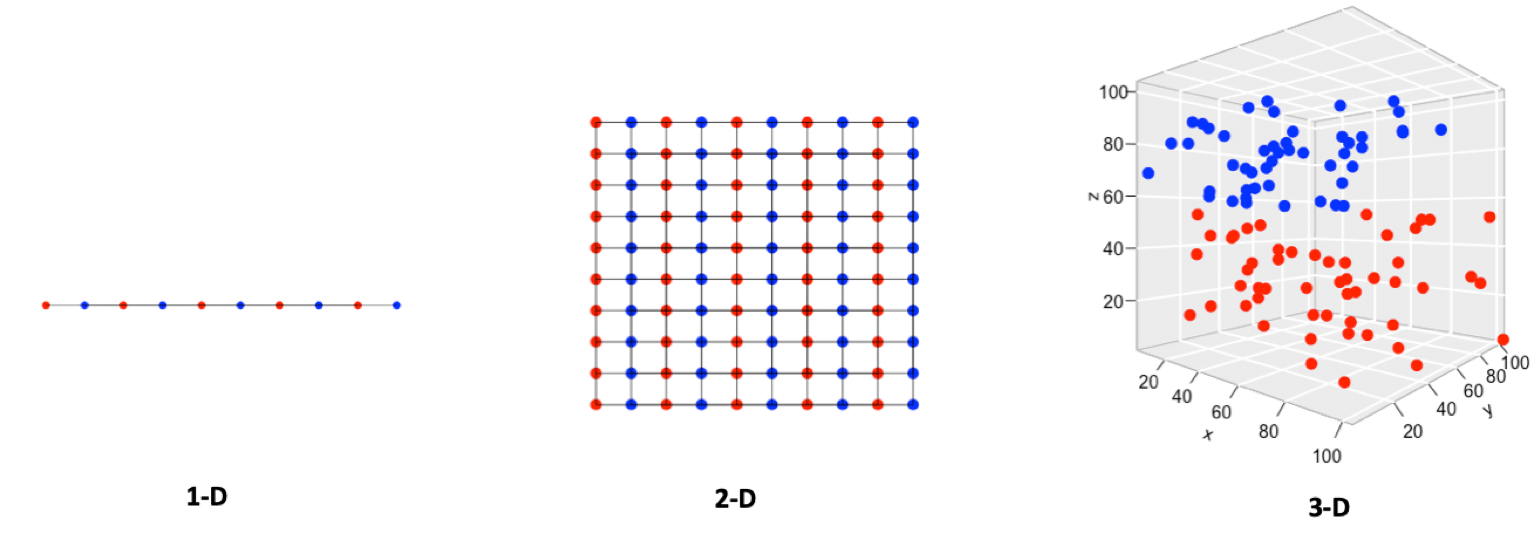
Heureusement, des techniques de réduction de dimension existent pour nous aider à projeter ces données de haute dimension dans un espace de plus faible dimension (souvent 2D ou 3D pour la visualisation) tout en préservant au maximum l’information pertinente ou la structure intrinsèque des données.

Parmi les méthodes les plus populaires, trois se distinguent particulièrement :

PCA (Principal Component Analysis) : Une approche linéaire classique, rapide et interprétable.
t-SNE (t-Distributed Stochastic Neighbor Embedding) : Une méthode non linéaire très efficace pour visualiser des clusters locaux.
UMAP (Uniform Manifold Approximation and Projection) : Une technique non linéaire plus récente, souvent plus rapide que t-SNE et offrant un bon équilibre entre structure locale et globale.

Dans cet article, nous allons explorer ces trois algorithmes, comprendre leurs principes fondamentaux, leurs avantages et inconvénients, et voir comment les appliquer en Python avec des exemples concrets. J’utiliserais le jeu de donnée MNIST qui est très simple mais montre bien les difficultés de visualisation pour un problème à haute dimension. Il est composé de 1797 petites images de taille 8 par 8, chaque pixel étant une dimension de notre problème on a alors 64 dimensions.

from sklearn.datasets import load_digits
digits = load_digits()
X = digits.data
y = digits.target
n_samples, n_features = X.shape
print(f"Dataset shape: {X.shape}")
# Dataset shape: (1797, 64)

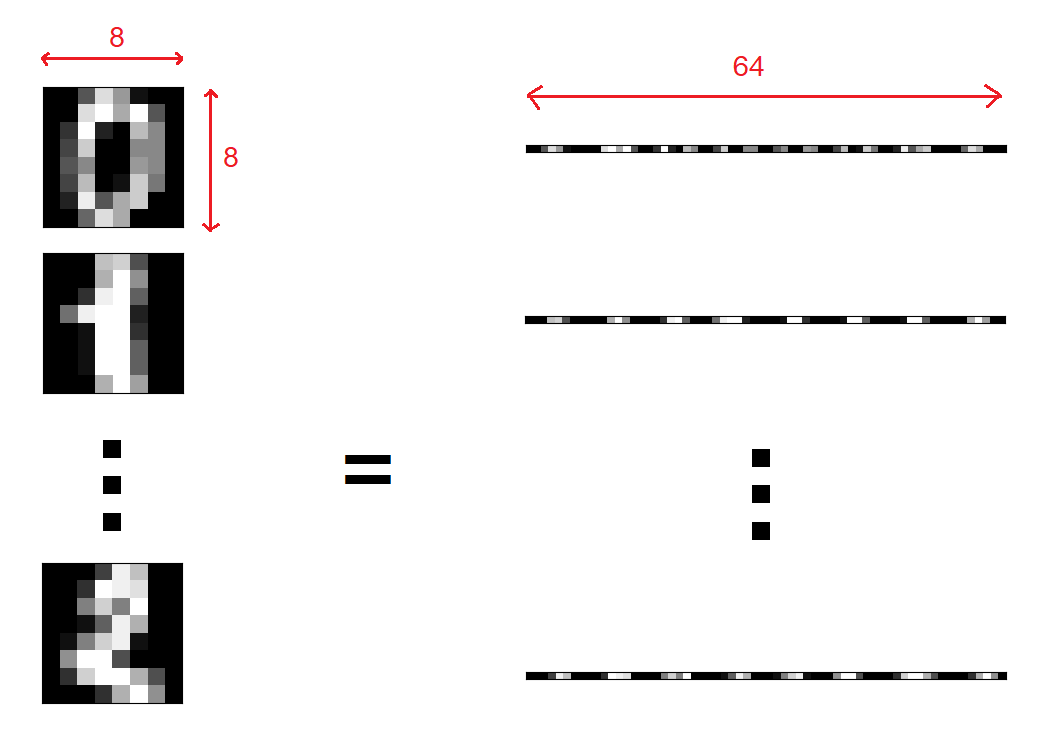
PCA : L’analyse en Composantes Principales

L’Analyse en Composantes Principales (PCA) est sans doute la technique de réduction de dimension la plus connue et utilisée. C’est une méthode linéaire qui vise à transformer les données originales en un nouvel ensemble de variables, appelées composantes principales, qui sont non corrélées entre elles et ordonnées selon la quantité de variance des données originales qu’elles expliquent.

L’idée maîtresse est de trouver les directions (axes) dans l’espace multi-dimensionnel le long desquelles les données varient le plus. La première composante principale est l’axe qui capture la plus grande variance. La deuxième composante principale est l’axe orthogonal au premier qui capture la plus grande partie de la variance restante, et ainsi de suite.

Mathématiquement, si $X$ est notre matrice de données centrées (chaque feature a une moyenne de 0), la matrice de covariance est donnée par $C = \frac{1}{N-1} X^T X$, où $N$ est le nombre d’échantillons. PCA cherche alors les vecteurs propres $v$ et les valeurs propres $\lambda$ de cette matrice $C$ qui satisfont l’équation :

\[C v = \lambda v\]

Les vecteurs propres $v$ (ordonnés par les valeurs propres $\lambda$ décroissantes) forment les directions des composantes principales. Les valeurs propres $\lambda$ indiquent la quantité de variance expliquée par chaque composante principale correspondante. La projection des données $X$ sur les $k$ premiers vecteurs propres $V_k = [v_1, v_2, …, v_k]$ donne la représentation réduite $X_{pca} = X V_k$.

# Standardize data (important for PCA)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# Apply PCA  to reduce to 2 dimensions
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)

print(f"Variance expliquée par composante: {pca.explained_variance_ratio_}")
print(f"Variance totale expliquée: {np.sum(pca.explained_variance_ratio_):.2f}")

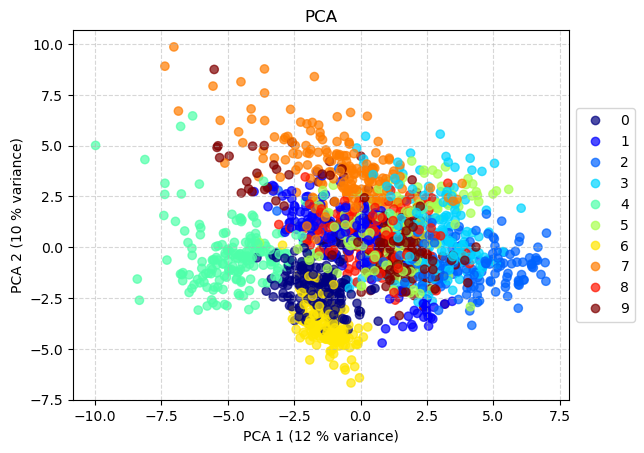
La PCA présente des avantages considérables : elle est simple, rapide et facile à calculer, offre une interprétabilité claire grâce à la quantification de la variance expliquée par chaque composante, et s’avère particulièrement efficace pour le débruitage et la compression de données. Cependant, cette méthode souffre de limitations importantes : elle suppose des relations linéaires entre les variables, se montre sensible à l’échelle des données (nécessitant une standardisation préalable), peine à capturer des structures non linéaires complexes comme les variétés courbes, et produit des composantes principales qui ne correspondent pas nécessairement aux features originales, compliquant parfois l’interprétation des résultats dans le contexte métier

Note: PCA maximise la variance globale. Si la structure intéressante des données ne se trouve pas dans les directions de plus grande variance, PCA peut la manquer.

t-SNE : Plongement Stochastique Distribué en t

Contrairement à la PCA, t-SNE (t-Distributed Stochastic Neighbor Embedding) est une technique non linéaire particulièrement conçue pour la visualisation de données de haute dimension en basse dimension (typiquement 2D ou 3D). Son objectif principal est de préserver la structure locale des données : les points qui sont proches dans l’espace de haute dimension devraient rester proches dans l’espace de basse dimension.

t-SNE modélise la similarité entre deux points $x_i$ et $x_j$ dans l’espace de haute dimension comme une probabilité conditionnelle $p_{j|i}$ que $x_i$ choisirait $x_j$ comme son voisin si les voisins étaient choisis en proportion de leur densité de probabilité sous une Gaussienne centrée sur $x_i$. Ensuite, il définit une probabilité de similarité jointe $p_{ij}$.

Dans l’espace de basse dimension, il modélise la similarité entre les points correspondants $y_i$ et $y_j$ avec une probabilité jointe $q_{ij}$ utilisant une distribution t de Student à un degré de liberté (qui est équivalente à une distribution de Cauchy). Cette distribution à queues lourdes permet de mieux séparer les points dissemblables dans la carte de basse dimension.

Plus formellement :

La probabilité conditionnelle $p_{j|i}$ est calculée comme : $p_{j\|i} = \frac{\exp(-\|x_i - x_j\|^2 / 2\sigma_i^2)}{\sum_{k \neq i} \exp(-\|x_i - x_k\|^2 / 2\sigma_i^2)}$ où $\sigma_i$ est la variance de la Gaussienne centrée sur $x_i$, déterminée de manière à correspondre à une perplexité fixée (liée au nombre effectif de voisins).
La probabilité jointe symétrique dans l’espace de haute dimension est : $p_{ij} = \frac{p_{j\|i} + p_{i\|j}}{2N}$ où $N$ est le nombre total de points.
La probabilité jointe dans l’espace de basse dimension $y_i, y_j$ utilise une distribution t-Student à 1 degré de liberté : $q_{ij} = \frac{(1 + \|y_i - y_j\|^2)^{-1}}{\sum_{k \neq l} (1 + \|y_k - y_l\|^2)^{-1}}$
L’algorithme minimise ensuite la divergence de Kullback-Leibler (KL) entre les distributions $P = {p_{ij}}$ et $Q = {q_{ij}}$ : $KL(P\|Q) = \sum_{i \neq j} p_{ij} \log \frac{p_{ij}}{q_{ij}}$ Cette minimisation est généralement effectuée par descente de gradient sur les positions des points $y_i$ dans l’espace de basse dimension.

# Apply t-SNE
from sklearn.manifold import TSNE
tsne = TSNE(n_components=2, perplexity=30, n_iter=300, random_state=42, n_jobs=-1)
X_tsne = tsne.fit_transform(X_scaled)

# Visualize
plt.figure(figsize=(10, 8))
scatter = plt.scatter(X_tsne[:, 0], X_tsne[:, 1], c=y, cmap=plt.cm.get_cmap("jet", 10), alpha=0.7)
plt.title('t-SNE des données Digits (perplexity=30)')
plt.xlabel('Composante t-SNE 1'), plt.ylabel('Composante t-SNE 2')
plt.legend(handles=scatter.legend_elements()[0], labels=digits.target_names)
plt.grid(True)
plt.show()

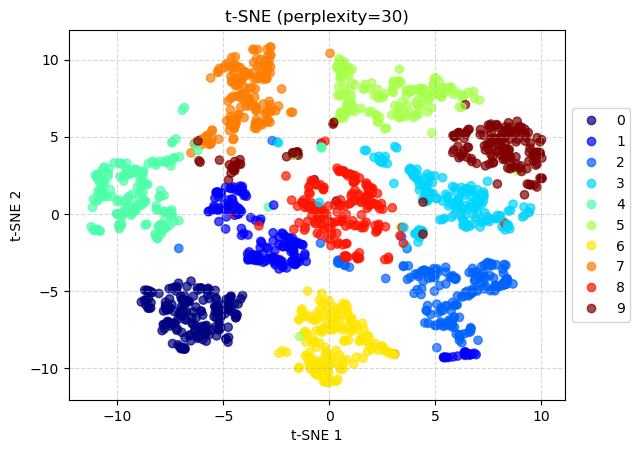
t-SNE présente des avantages remarquables pour l’analyse exploratoire des données : il excelle dans la révélation de la structure locale et des clusters, capture efficacement les structures non linéaires complexes que d’autres méthodes peinent à identifier, et constitue un outil largement adopté pour la visualisation exploratoire. Néanmoins, cette technique souffre de plusieurs limitations significatives : elle est coûteuse en calcul avec une complexité typiquement de $O(N^2)$ ou $O(N \log N)$ avec approximations, ce qui peut ralentir considérablement l’analyse sur de très grands datasets. Sa nature stochastique implique que différentes exécutions peuvent produire des visualisations légèrement différentes, nécessitant de fixer le random_state pour assurer la reproductibilité. t-SNE se montre particulièrement sensible aux hyperparamètres, notamment la perplexity (liée au nombre de voisins considérés, typiquement entre 5 et 50) et le nombre d’itérations n_iter, obligeant souvent à expérimenter pour obtenir des résultats satisfaisants. Plus fondamentalement, cette méthode ne préserve pas bien la structure globale : la taille et les distances entre les clusters dans la visualisation t-SNE ne sont généralement pas significatives et ne peuvent être interprétées comme dans PCA. Enfin, t-SNE demeure principalement une technique de visualisation plutôt qu’une véritable méthode de réduction de dimension pour l’entraînement de modèles, car elle n’est pas définie sur de nouveaux points.

Attention: N’interprétez pas trop la taille relative des clusters ou les distances entre eux dans un graphique t-SNE. Concentrez-vous sur les groupements de points similaires.

UMAP : Approximation et Projection Uniforme de Variétés

UMAP (Uniform Manifold Approximation and Projection) est une technique de réduction de dimension non linéaire plus récente qui gagne rapidement en popularité. Comme t-SNE, elle est efficace pour la visualisation, mais elle est souvent plus rapide et prétend mieux préserver la structure globale des données.

UMAP est basé sur des fondements mathématiques solides issus de la topologie algébrique et de la théorie des variétés riemanniennes. L’algorithme fonctionne en trois étapes principales :

Construction d’un graphe de voisinage pondéré : Pour chaque point, UMAP trouve ses $k$ plus proches voisins et construit une représentation pondérée de la structure topologique locale des données (une “variété floue”).
Calcul d’une représentation bas-dimensionnelle similaire : UMAP répète le processus de construction de graphe dans l’espace de basse dimension cible.
Optimisation : UMAP minimise la différence (entropie croisée) entre les représentations topologiques de haute et basse dimension, cherchant ainsi une projection qui préserve au mieux la structure topologique des données originales.

UMAP est disponible en python en l’installant simplement avec la commande suivante:

pip install umap-learn

# Apply UMAP
import umap
reducer = umap.UMAP(n_neighbors=10, min_dist=0.1, n_components=2, random_state=42)
X_umap = reducer.fit_transform(X_scaled)

# Visualize
plt.figure(figsize=(10, 8))
scatter = plt.scatter(X_umap[:, 0], X_umap[:, 1], c=y, cmap=plt.cm.get_cmap("jet", 10), alpha=0.7)
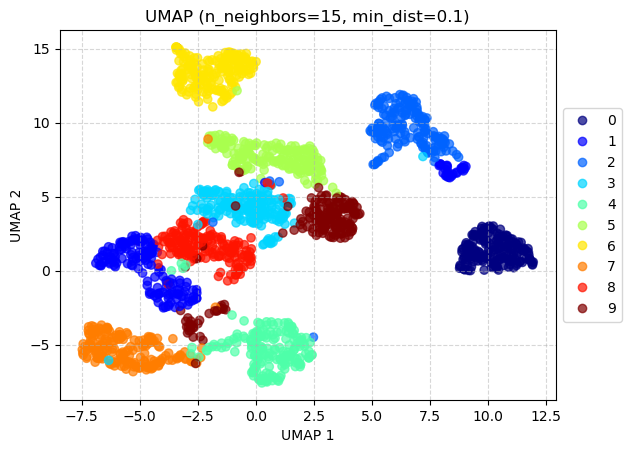
plt.title('UMAP des données Digits (n_neighbors=15, min_dist=0.1)')
plt.xlabel('Composante UMAP 1'), plt.ylabel('Composante UMAP 2')
plt.legend(handles=scatter.legend_elements()[0], labels=digits.target_names)
plt.grid(True)
plt.show()

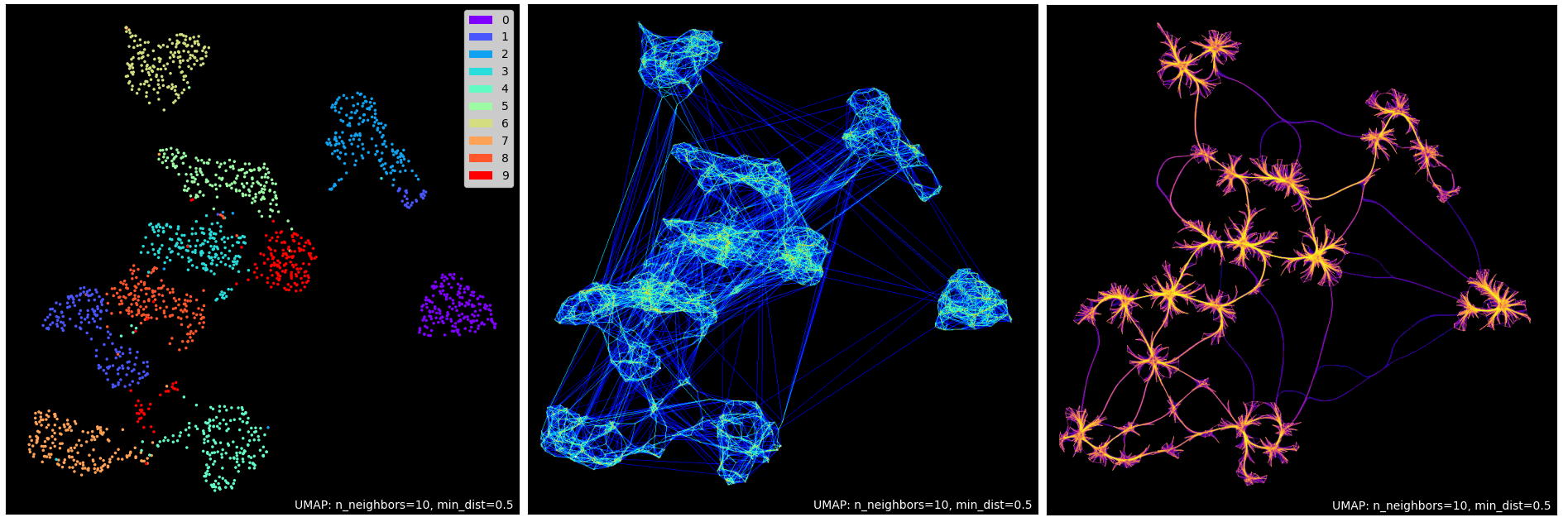
De plus, le package umap intègre des outils de visualisation très simples permettant de génère des graphes pour mieux comprendre les structures locales et globales de nos données.

import umap.plot
umap.plot.points(reducer, labels=y, theme='fire')
umap.plot.connectivity(reducer, show_points=True, background="black", values=X_umap.mean(axis=1), edge_cmap="jet")
umap.plot.connectivity(reducer, edge_bundling='hammer', background="black", edge_cmap="plasma")

UMAP présente des avantages substantiels qui en font une alternative attrayante aux méthodes classiques : il est souvent significativement plus rapide que t-SNE, particulièrement sur de grands datasets, et offre un bon équilibre entre structure locale et globale en tendant à mieux préserver la structure globale des données que t-SNE tout en excellant dans la capture de la structure locale. Cette méthode se montre moins sensible aux hyperparamètres, ses paramètres par défaut (n_neighbors=15, min_dist=0.1) fonctionnant souvent bien même si l’expérimentation reste recommandée, et produit des résultats déterministes reproductibles avec le même random_state. Un atout majeur d’UMAP réside dans sa capacité à être utilisé au-delà de la simple visualisation, la transformation étant définie pour de nouveaux points et permettant une véritable réduction de dimension pour l’entraînement de modèles. Cependant, UMAP présente aussi certaines limitations : étant plus récent, sa théorie sous-jacente est plus complexe à appréhender que celle de PCA, l’interprétation des distances reste délicate bien que potentiellement plus significative que pour t-SNE, et comme ce dernier, il demeure sensible au choix des métriques de distance lorsque les données ne sont pas numériques standard.

Conseil: UMAP est souvent un excellent point de départ pour la visualisation non linéaire, offrant un bon compromis entre vitesse, qualité de la séparation des clusters et préservation de la structure globale.

PCA vs t-SNE vs UMAP : Lequel choisir ?

Il n’y a pas de “meilleure” méthode universelle ; le choix dépend de vos données et de votre objectif :

Caractéristique	PCA	t-SNE	UMAP
Type	Linéaire	Non linéaire	Non linéaire
Objectif principal	Max variance, compression, débruitage	Visualisation structure locale (clusters)	Visualisation équilibre local/global
Structure globale	Préservée (si linéaire)	Généralement non préservée	Mieux préservée que t-SNE
Structure locale	Peut être perdue	Très bien préservée	Très bien préservée
Vitesse	Très rapide	Lente (surtout N grand)	Rapide (souvent > t-SNE)
Interprétabilité	Élevée (variance expliquée)	Faible (distances inter-clusters non fiables)	Modérée (distances potentiellement + fiables)
Stochasticité	Déterministe	Stochastique	Déterministe (par défaut)
Hyperparamètres	`n_components`	`perplexity`, `n_iter`, `learning_rate`	`n_neighbors`, `min_dist`
Usage pré-processing	Oui	Non (généralement)	Oui (possible)

En résumé :

Commencez par PCA si vous suspectez des relations linéaires, si vous avez besoin d’interprétabilité ou si la vitesse est critique. C’est aussi une bonne étape de pré-processing pour réduire le bruit avant d’appliquer t-SNE ou UMAP.
Utilisez t-SNE si votre objectif principal est de visualiser des groupements fins et la structure locale dans vos données, et si le temps de calcul n’est pas une contrainte majeure. Soyez prudent avec l’interprétation des distances globales.
Essayez UMAP comme alternative moderne à t-SNE. Il est souvent plus rapide, gère mieux les grands datasets et offre un meilleur équilibre entre la préservation des structures locales et globales. C’est un excellent choix par défaut pour la visualisation non linéaire.

Il est souvent instructif d’appliquer plusieurs de ces méthodes et de comparer les résultats pour obtenir une compréhension plus complète de la structure de vos données. Le site https://projector.tensorflow.org/ offre un playground interactif pour visualiser en 3D des données images et textuelles sur les 3 algorithmes décrits dans ce post. Amusez-vous bien !