Segmentation d’objets par modèle de Deep Learning
Contexte
Le projet est de développer un algorithme qui détecte sur des images 2D les pixels appartenant à la face avant de la monture portée par l’utilisateur en étant robuste le plus possible à tous les différents types de monture qui peuvent exister ainsi que les différentes positions que peut avoir l’utilisateur devant la caméra. On parle ici d’un problème de segmentation, contrairement à la tâche de classification où le but est simplement d’identifier si oui ou non l’objet recherché est présent dans les images.
La détection de lunettes est un problème clé pour la recherche de vision par ordinateur dû à sa relation directe avec les systèmes de reconnaissance faciale. Le problème fut typiquement approché en localisant la zone des yeux et en caractérisant les régions alentours. Une combinaison de techniques morphologiques du traitement d’images fut testée pour décrire la zone des lunettes comme l’utilisation de motif binaire locaux [1], la décomposition en ondelette [30], les histogrammes de gradient orienté [31] ou encore les caractéristiques pseudo-Haar [32]. Ces approches demandent une expertise fine du domaine et connaissent de vraies limitations pour obtenir une segmentation complète pour tous les types de montures existants et sous toutes les conditions de positions et d’environnement. Ces dernières années, les approches d’apprentissage profond ont été largement utilisées et ont permis de grande avancées dans le domaine de la vision par ordinateur. Elles ont l’avantage d’être agnostiques aux problèmes à résoudre mais nécessitent en contrepartie une base de données annotées au préalable. Saddam BEKHET [33] présente un modèle robuste pour classifier des images avec ou sans lunettes dans des conditions difficiles mais ne segmente pas précisément la monture. Cheng-Han LEE et al. [28] fournissent un jeu de données annotées pour la segmentation de 19 classes du visage (nez, bouche, cheveux …), il est composé de plus de 30 000 images. On trouve parmi ces 19 classes, la classe “lunette” définie comme l’ensemble des éléments de la lunette (monture, verre, branche) alors que notre problème exige uniquement une segmentation de la face avant de la monture (pas le verre ni les branches).
L’approche retenue pour le problème de segmentation de la face avant de la monture est celle de l’apprentissage supervisée avec notamment 2 approches. Une première s’appuyant sur un jeu de données générées synthétiquement et permettant d’avoir accès à une grande quantité d’images annotées. Et une deuxième se basant sur un jeu de données réelles ayant été annotées manuellement et plus spécifique au cas d’application mais avec une faible quantité d’image. Un rappel du fonctionnement général des réseaux de neurone sera fait puis plus spécifiquement sur les architectures propres à la segmentation sémantique dans le chapitre [Etat de l’art]. Ensuite, les différentes expériences effectuées seront présentées dans le chapitre [Travaux]. Enfin, les résultats seront discutés et les potentielles améliorations énumérées dans le chapitre [conclusion].
État de l’art
Architectures pour la Segmentation Sémantique
Dans un réseau de neurones spécialisé dans la classification, le type d’information est encodé mais pas sa position précise. En effet, les opérations de pooling effectuent un sous-échantillonnage de l’information et permettent au modèle de comprendre le type d’information présent dans l’image mais la position de l’information est perdue au cours du procédé. Comme expliqué en introduction, dans le contexte du stage, la tâche à effectuer est celle de la segmentation. L’objectif de la segmentation sémantique est d’étiqueter chaque pixel d’une image par sa classe correspondante. Contrairement à la tâche de classification qui consisterait à dire si oui ou non il existe une monture dans l’image, la dimension de sortie est alors bien inférieure à la dimension d’entrée (en général).

Différentes tâches de reconnaissance d'image. La segmentation d'instance est la plus complexe.
Pour la segmentation, la dimension de sortie est quasiment identique à celle d’entrée puisqu’elle correspond exactement à la taille de l’image. Le challenge principal est de retrouver où se trouve l’information dans l’image en effectuant du sur-échantillonnage pour récupérer une sortie de la même taille que l’image d’entrée. Pour se faire, de nombreuses techniques du traitement d’images classique sont connues comme l’interpolation bilinéaire, l’interpolation aux plus proches voisins, le unpooling, la convolution transposée (ou déconvolution)… Comme vous vous en doutez, l’opération retenue pour un réseau de neurones convolutionnel est souvent la convolution transposée puisqu’on va pouvoir apprendre les paramètres grâce à nos données et avoir un sur-échantillonnage adapté au problème. L’idée est de réaliser l’opération inverse de la convolution : en partant du produit et du filtre, retrouver l’image d’origine.
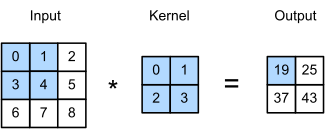
(a) Convolution.

(b) Convolution transposée.
Exemples de calculs de convolution classique (a) et transposée (b).
Une majorité des architectures des réseaux de neurones pour la segmentation sont constituées d’une partie encodeur qui encode l’information avec des opérations de convolution et de pooling puis d’une partie décodeur qui décode l’information spatialement en utilisant des opérations de déconvolution et de unpooling. Au final, on obtient un réseau de neurones constitué uniquement de couches convolutionnelles et ne contenant aucune couche dense, ce qui permet d’accepter en entrée des images de n’importe quelle taille. On peut, par exemple, tester des images de taille différentes lors du test et lors de l’entraînement. Dans les sections suivantes, des architectures spécifiques et reconnues seront citées pour mieux comprendre les enjeux rencontrés lors des problèmes de segmentation d’image.
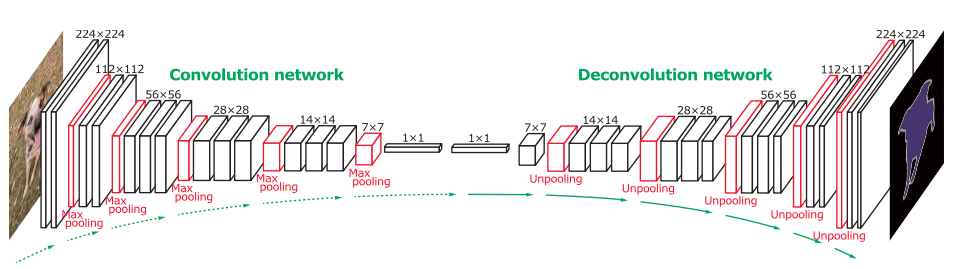
Architecture complètement convolutionnelle (FCN) pour la segmentation
UNet
L’architecture UNet [6] a été développée par O. Ronneberger en 2014 pour de la segmentation d’images biomédicales. Comme discuté précédemment pour les architectures de segmentation, il y a deux parties principales : l’encodeur qui sous-échantillonne l’information et permet de savoir ce qui est dans l’image et le décodeur qui sur-échantillonne et permet de savoir où est l’information dans l’image. Le principal ajout par rapport à ce qui a été précédemment énoncé est le fait de connecter les couches de même niveau de résolution de l’encodeur et du décodeur. En effet, en concaténant les 2 informations puis en appliquant 2 opérations de convolution, le modèle a une information supplémentaire et peut apprendre comment sur-échantillonner de façon plus efficace.
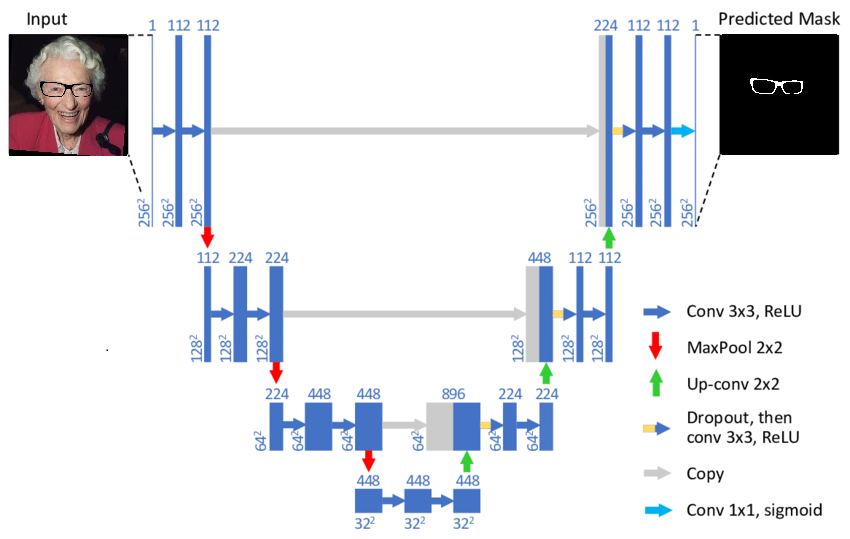
Architecture UNet
PSPNet
L’architecture PSPNet (Pyramid Scene Parsing) [7] développée en 2016 par H. ZHao et al. de CUHK et l’entreprise Sensetime a réalisé des performances “state-of-the-art” sur les benchmark d’ImageNet 2016 scene parsing challenge, PASCAL VOC 2012 et Cityscapes. En observant les mauvaises prédictions faites par un CNN, ils ont conclu que le modèle avait besoin de plus d’information globale de l’image. En effet, il remarque par exemple que le modèle prédit un bateau sur l’eau comme une voiture en se basant sur son apparence alors que le sens commun nous dit qu’une voiture a peu de chance de flotter sur l’eau. Pour décrire cette information globale de l’image, l’encodeur de PSPNet utilise des couches de convolutions dilatées qui aident à augmenter le champ récepteur des features. Ensuite des features de différentes tailles sont regroupées par des opérations de pooling. Ces différentes échelles de contexte sont directement sur-échantillonnées avec des interpolations bilinéaires pour être concaténées et formées un seul volume encodant différents contextes d’information. Ce volume est finalement passées à une couche de convolution pour générer la prédiction finale.
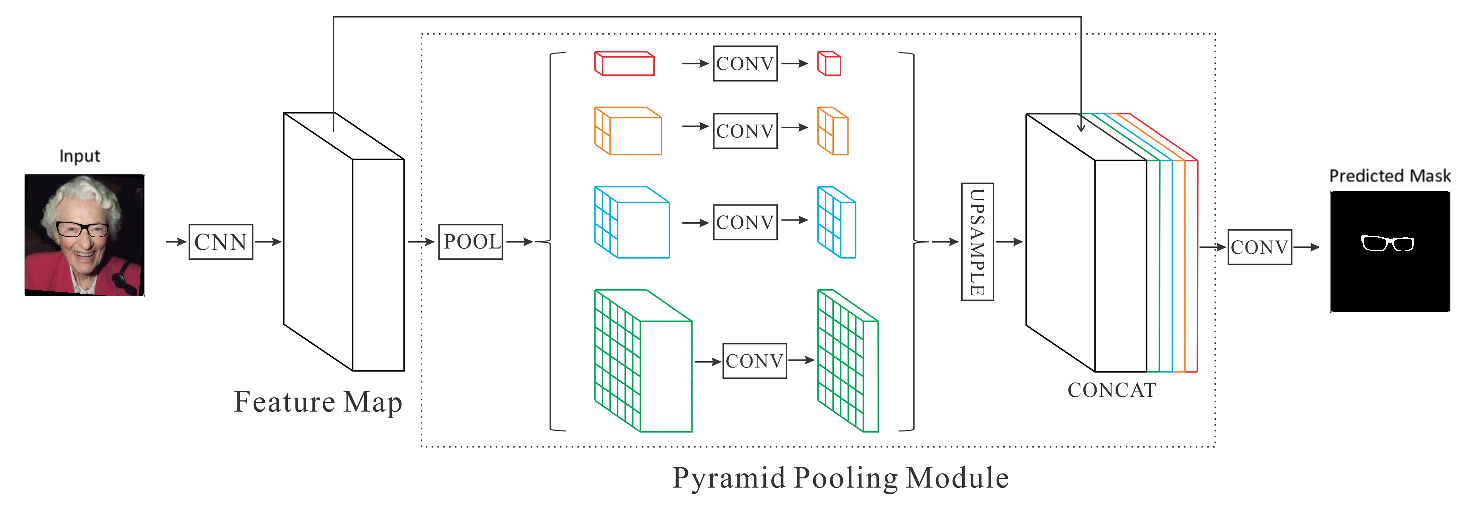
Architecture PSPNet
DeepLab
DeepLab [12] est une architecture développée la même année que PSPNet et réalise également des performances du même ordre de grandeur puisque l’idée et les techniques utilisées sont semblables. Elle est notamment connue pour introduire précisément la notion des convolutions dilatées (ou atrous convolution) pour aider à encoder l’information locale et globale de l’image. D’autre part, DeepLab a subi plusieurs améliorations depuis sa création et 3 versions existent actuellement. Les convolutions dilatées ([fig:atrous_convolution]) permettent d’élargir le champ récepteur des filtres et donc de se passer de toutes les couches de déconvolution pour la partie décodage utilisées dans les réseaux complètement convolutionnels (UNet, FCN …) mais DeepLab V1 est contraint de faire passer la sortie des convolutions dilatées dans une interpolation bilinéaire et un modèle CRF.
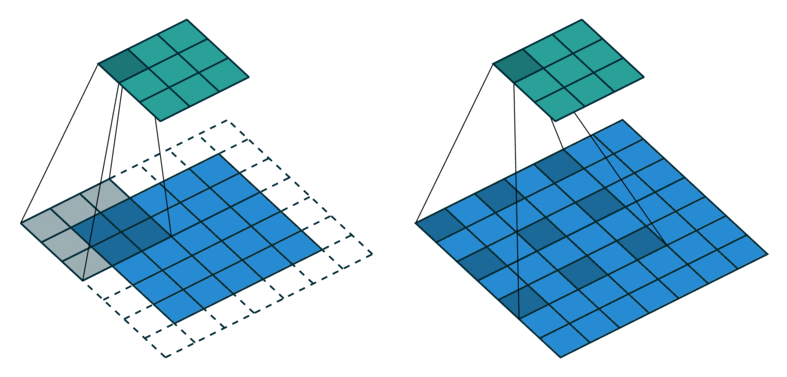
A gauche, convolution standard. A droite, convolution dilatée (avec un taux de dilatation de 2).
L’idée de DeepLab V2 est, de la même manière que PSPNet, d’effectuer un pooling spatial pyramidal dilaté (ASPP) en appliquant de multiples convolutions dilatées avec des taux d’échantillonnage différents (exemple : 4 kernels 3x3 avec des taux de 6, 12, 18 et 24) et de concaténer les sorties en un seul volume, ce qui aide à prendre en compte différentes échelles d’objet. Enfin, DeepLab V3 [13] et V3+ se concentre sur la capture de frontières plus nettes pour la segmentation des objets. En effet, jusqu’ici le modèle utilisait une interpolation pour le sur-échantillonnage et non un décodeur avec des convolutions comme dans UNet. En utilisant une partie décodeur peu profonde qui exploite les convolutions dilatées, le modèle obtient des résultats plus précis et nets autour des objets segmentés.
BiseNet
BiseNet [14] est une architecture développé en 2018 par une équipe chinoise ayant pour but de trouver un équilibre entre performance et vitesse d’inférence. En effet, pour accélérer un modèle on peut choisir de : réduire la taille de l’entrée (en rognant ou redimensionnant l’image), réduire les channels du réseau ou supprimer les dernières couches mais à chaque fois au détriment de la perte de détails spatiaux. BiseNet propose alors un réseau avec 2 parties : Spatial Path (SP) et Context Path (CP). Le Spatial Path empile 3 couches convolutionnelles pour obtenir une feature map 1/8 et le Context Path ajoute une couche de global average pooling à la fin de Xception où le champ récepteur est maximum. Ensuite pour fusionner ces 2 informations et raffiner la prédiction, des modules appelés Feature Fusion (FFM) et Attention Refinement (ARM) sont respectivement développés.
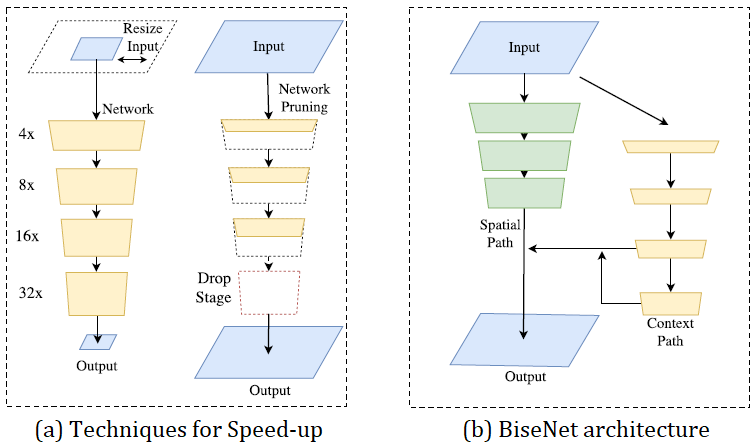
Architecture BiseNet
Métriques et fonctions Loss
La première métrique qu’on peut évaluer pour la tâche de segmentation est la précision (accuracy) au niveau pixel qui consiste simplement au pourcentage de pixels de l’image qui sont classifiés correctement. Cette métrique peut être pertinente pour des cas où les classes sont distribuées de façon équilibré sur l’image mais lorsque notre problème est déséquilibré et qu’une classe domine largement l’image et une autre occupe seulement une petite portion, le score de précision peut être trompeur puisqu’une prédiction qui donnerait la valeur de la classe dominante à l’image entière aurait un très bon score.
![]()
Exemple de classe déséquilibré où le score de précision est inefficace. En prédisant l'image entière comme du background, on obtient quand même une précision de 90%.
Le score IoU\footnote{Intersection Over Union} aussi appelé indice de Jaccard est l’une des métriques les plus utilisée en segmentation sémantique puisqu’elle exprime l’aire de chevauchement entre prédiction et vérité divisé par l’aire d’union des deux. Elle peut être calculée ainsi : \(\text{IoU} = \frac{TP}{TP+FP+FN}\) où $TP$ désigne les vrais positifs, $FP$ les faux positifs et $FN$ les faux négatifs. Si on reprend l’exemple de la figure [accuracy], on a 90% de chevauchement pour la classe background mais 0% pour la classe lunette, on obtient donc au final un score IoU de 45% ce qui paraît un peu plus approprié pour la prédiction proposée. Pour un problème binaire comme celui de notre problème, on pourra calculer le score IoU seulement de la classe lunette (pour des problèmes multi-classes, on peut également exclure le background). Une grandeur qui revient également souvent pour la segmentation et qui est très proche de l’IoU est le coefficient Dice (ou F1 score) : \(\text{Dice} = \frac{2TP}{2TP+FP+FN}\) Ces deux métriques sont corrélées positivement, c’est-à-dire que pour une unique donnée si un classifieur A est meilleur qu’un classifieur B sous l’une des métriques alors il sera également meilleur que B sous l’autre métrique. La différence entre les deux vient quand on compare les deux sur un ensemble de données. En général, la métrique IoU pénalise plus fortement les mauvaises segmentation que le coefficient Dice. On peut penser au coefficient Dice comme une métrique qui mesure une performance moyenne alors le score IoU mesure quelque chose qui s’approche plus de la pire performance.
Les problèmes de classification d’images basées sur des CNN sont typiquement entraînés en minimisant la cross-entropie (page \pageref{CE}) qui mesure une affinité entre la probabilité sortie du réseau et le label. La cross-entropie standard a des inconvénients bien connus pour des problèmes où la distribution des classes sont fortement déséquilibrées, il en résulte des entraînements instables et des frontières de décision biaisées envers la classe majoritaire. Pour les tâches de segmentation, les métriques de score évoquées précédemment peuvent être directement utilisé comme fonction de Loss en utilisant $1 - \text{IoU}$ ou $1 - \text{Dice}$ pour bien avoir un problème de minimisation. En effet, comme expliqué précédemment, elles surpassent les performances de la cross-entropie et sont plus robustes aux problèmes déséquilibrés et en plus, elles permettent au réseau non pas de se concentrer sur le résultat de chaque pixel mais sur la forme globale de l’objet de la segmentation.
Expériences
L’objectif des travaux est la segmentation de monture de lunettes pour un instrument de mesure. Seule la face avant de la lunette est considérée dans ces travaux puisque les mesures nécessaires pour l’instrument concernent seulement le plan vertical avant de la monture. Les branches ainsi que les verres ne seront donc pas concernés par la segmentation. De plus, le problème est binaire puisqu’il existe 2 classes : la monture et le background.
Dû à l’absence d’une base de données annotées de qualité suffisante et de taille suffisante, les sujets de l’apprentissage semi-supervisé et des réseaux génératifs (GAN) ont été abordés. Le premier permet d’utiliser un petit jeu de données annotées et d’exploiter un grand nombre de données non annotées, le second permet de générer des images sans utiliser d’annotation. Ces approches ont été abandonnées, d’une part du fait de leur complexité et d’autre part, l’apport en performance qu’elles peuvent procurer est faible comparé à celui d’une base de données annotées de qualité.
L’approche retenue ici est finalement celle de l’apprentissage supervisé avec les architectures de réseau de neurones convolutionnel propres à la segmentation (cf section [segmentation]). Pour la phase d’apprentissage, deux approches ont été mises en place. La première est d’utiliser des images synthétiques où la monture a été apposée automatiquement sur le visage d’une personne. La deuxième approche est de constituer manuellement une base de données en étiquetant chaque image collectée. Avant de décrire les expériences réalisées, un bref rappel des travaux précédemment testés au sein de l’entreprise sera fait. Les différentes technologies logiciel et matériel seront également énumérées.
Données synthétiques
Base de données
Une première partie des travaux fut d’utiliser des données synthétiques pour la base d’apprentissage. En effet, aucune base de données annotées correspondant à la segmentation voulue existe au sein de l’entreprise ou en open-source. Ces données synthétiques sont générées avec le même outil de Virtual Try On (VTO) cité en section [previous_work]. Cet outil utilise les landmarks du visage pour y superposer une image de lunette sur la zone des yeux. Avec ce procédé, il est possible de connaître exactement les pixels modifiés et donc d’avoir l’étiquette associée à chaque image nécessaire pour l’apprentissage supervisé. La base de donnée publique Labeled Faces in the Wild [23] composée de \textasciitilde 10 000 images (et \textasciitilde 5000 personnes différents) a été utilisée. Les images sont de taille 250*250 pixels. Pour chaque image, une monture choisie aléatoirement parmi 50 a été placée avec le VTO. Ainsi, la base de donnée obtenue est assez variée avec beaucoup de visages différents chacun dans des conditions différents (position, luminosité, arrière-plan). Aucun pré-traitement n’est appliqué sur l’image comme ce fut le cas dans les travaux précédents.

Images.

Masques.
Base de donnée d'apprentissage générée à partir du VTO.
Entrainements
Une architecture Unet avec un encodeur Resnet est choisie pour être entraînée sur ce jeu de données. Les poids de l’encodeur sont pré-appris sur ImageNet. Les images en entrées sont normalisées de la même façon que les images de ImageNet (\path{mean=[0.485,0.456,0.406]} et \path{std=[0.229,0.224,0.225]}). Le coefficient Dice est utilisé comme Loss et le score IoU comme métrique. La descente de gradient stochastique par mini-batch est utilisée. Les paramètres d’optimisation ont été grossièrement ajustés par RandomSearch : taille de batch $32$, momentum $0.99$, weight decay $10^{-4}$, learning rate $0.01$. La valeur du learning rate est gardée constante tout le long de l’entraînement. Le nombre d’epoch est fixé à 200 epochs. $80 \%$ du jeu de données est utilisé pour l’entraînement et $20 \%$ pour le test. Le meilleur score et le meilleur modèle sont sauvegardés en mémoire et mis à jour à chaque itération, ce qui peut permettre d’éviter l’overfitting (on parle d’Early Stopping).
Finalement, le meilleur score IoU moyen obtenu sur le jeu de train est de $81.59 \%$ et $\boldsymbol{83.88 \%}$ sur le test. Pour information, la matrice de confusion est affichée en figure [fig:confusion_matrix]. Pour la tâche de segmentation, on ne cherche pas spécialement à faire plus ou moins un certain type d’erreur c’est pourquoi les métriques telles que la précision ou le rappel ne sont pas mis en avant et que le score IoU moyen est principalement utilisé pour mesurer la performance du modèle.
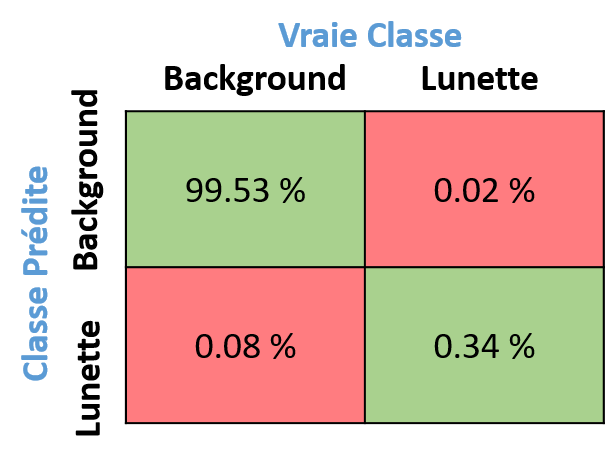
Matrice de confusion
Un tel score pour un problème de segmentation est largement satisfaisant visuellement. Il est difficilement améliorable notamment parce que le jeu de données utilisé comporte certaines limitations : avec le VTO, la lunette est parfois placée dans des positions irréelles (par-dessus un autre objet, à l’envers, mauvaise perspective) et des artefacts de compression sont rajoutés à l’image et au label (cf. figure [fig:quality_data]).

Positions des montures

Artefact de compression
Limites du jeu de données synthétiques
Le modèle obtenu a ensuite été testé sur les quelques images réelles à disposition qui avaient pu être annotées à cet instant du projet. Sur ces images, la prédiction est visuellement bien moins précise (cf. figure [fig:prediction_VTO_batch]) et le score moyen IoU est de $\boldsymbol{20 \%}$ (calculé à partir d’une cinquantaine d’image réelle annotée). Les résultats ne parviennent pas à être généralisés à ces nouvelles données, la raison la plus probable est que les données sont trop différentes l’une de l’autre. En effet, les montures ajoutées virtuellement ne sont pas intégrées dans l’image de la même façon que les montures réelles : le bruit, les textures, les ombres, les reflets, les perspectives, les branches sont des éléments différents entre les 2 jeux de données. On peut penser notamment que le modèle overfitte les basses fréquences présentes dans les images de montures ajoutées virtuellement et absentes dans les images réelles. L’idée d’utiliser des données synthétiques peut être une bonne idée mais il faudrait passer du temps à améliorer l’outil pour que les images générées soient le plus proche possible de la réalité du problème. Dans les travaux suivants, on s’intéresse à la performance du réseau sur une base de données réelles manuellement annotées.

Données synthétiques - score $83\%$

Données réelles - score $20\%$
Prédiction (rouge) sur un batch de données
Données réelles
Base de données
Comme discuté précédemment, le choix a été fait de prendre le temps d’annoter manuellement des images enregistrées par l’instrument de mesure. Ces images sont tirées de vidéos enregistrées dans un magasin d’opticien prototype au sein des locaux de l’entreprise selon un protocole précis dans des conditions de test réelles. Elles nous sont envoyées au fur et à mesure que des clients acceptent d’utiliser l’instrument. Au final, 66 vidéos de personnes différentes ont pu être collectées, chacune de ces personnes portent des montures différentes. Les montures sont portées sans verre. L’un des objectifs principaux de l’étude étant de développer un outil de segmentation de monture robuste aux différentes positions, 3 à 4 images ont été extraites des vidéos. Chacune de ces images ont été sélectionnées de sorte que l’angle de tête soit suffisamment différents l’un de l’autre (cf. figure [fig:nature_dataset]). La base de données d’images est finalement constituée de 185 images de tailles 1280720 ou 19201080 pixels (selon la configuration de l’instrument lors de la prise de mesure). Chaque fichier est différentiable par un nom unique composé comme suit : \texttt{xxx_scanRecord_yy.jpg}. Les 3 premiers caractères identifient la personne et les 2 derniers le numéro de l’image dans la vidéo originale. Pour les expériences qui suivent, l’ensemble des données est divisé en train/test/validation avec les proportions 0.8/0.1/0.1 en faisant attention à ce que les images d’une même personne ne se retrouvent pas à la fois dans le train et dans le test. Au final, l’ensemble de train est constitué de 145 images (52 personnes), l’ensemble test de 15 images (6 personnes) et l’ensemble de validation de 25 images (8 personnes).
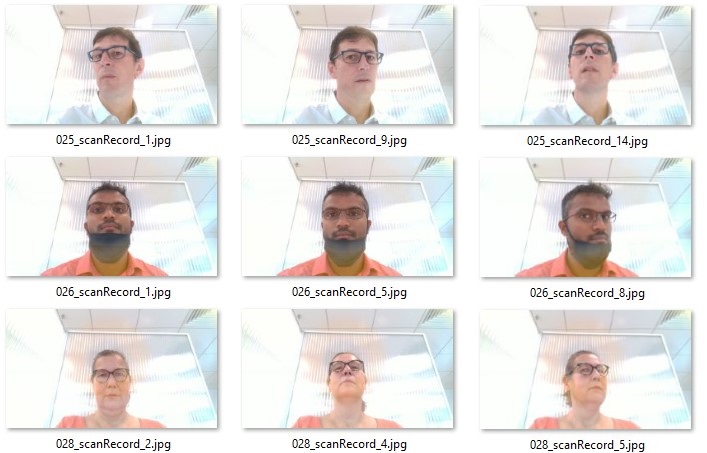
Batch de donnée réelle
Pour l’étape de labellisation, différents outils pouvant faire de la segmentation ont été étudiés (cf. table [tab:label_tool]). Les principaux critères d’utilisation sont le type de ligne disponible, le format de sortie, la connectivité et la prise en main. Étant donné que les montures de lunette sont constituées majoritairement de formes arrondies, il paraissait donc intéressant de pouvoir tracer des courbes de bézier pour épouser au mieux le contour de la monture. Cependant après plusieurs essais l’idée a été abandonnée puisque le traçage de courbes de Bézier n’est finalement pas très intuitif à prendre en main pour un débutant et la perte de temps associée est non négligeable : \textasciitilde 10min/image en utilisant des courbes de bézier contre \textasciitilde 3min30/image en utilisant des polygones. La sortie de la plupart des outils se présente sous la forme d’un fichier json donnant la position de chaque point tracé qu’il faut par la suite transformer en image binaire (1 pour la monture et 0 pour l’arrière-plan). Ensuite, la possibilité d’utiliser l’outil en ligne et sa facilité d’installation a été également un critère important puisqu’il avait été imaginé de mettre à contribution un maximum de personnes pour gagner du temps. Finalement, l’outil choisi est VIA [via] (BSD 2-Clause License) pour sa facilité de prise en main ainsi que sa possibilité d’être installé et utilisé hors ligne (en html). En effet, l’outil de labellisation a été utilisé hors-ligne permettant de s’assurer que les données personnelles (les images) ne soient pas transférées et stockées sur un serveur distant. L’idée de faire appel à une société externe spécialisée dans la tâche d’annotation d’images à également été abordée pour pouvoir labelliser plus d’images en un temps réduit, cette piste a été mise de côté pour le sujet du stage mais n’est pas exclue pour des travaux ultérieurs.
\begin{table}[H]
\centering
\small
\begin{tabular}{||c | c | c | c | c||}
\hline
\rowcolor{lightgray}
nom & type de ligne & format de sortie & connectivité & prise en main \ [0.5ex]
\hline\hline
\href{https://github.com/wkentaro/labelme}{labelme} & polygone & json & hors ligne & ++ \
\hline
\href{https://github.com/openvinotoolkit/cvat}{CVAT} & polygone & json, xml & en ligne, hors ligne & ++
\hline
\href{https://labelbox.com/}{labelbox} & polygone, main levé & json, csv & en ligne & +
\hline
\href{https://www.makesense.ai/}{makesense.ai} & polygone & json & en ligne & +
\hline
\href{https://www.scalabel.ai/doc/index.html}{scalabel} & polygone, bézier & json & hors ligne & -\ -
\hline
\href{http://www.robots.ox.ac.uk/~vgg/software/via/via.html}{VIA} & polygone & json & hors ligne, en ligne & +++ \
\hline
\href{https://inkscape.org/}{inkscape} & polygone, bézier & png & hors ligne & -
\hline
\end{tabular}
\caption{Fonctionnalités de différents outils de labellisation.}
\label{tab:label_tool}
\end{table}
Entrainements
Étant donné que le jeu de données réelles est beaucoup plus petit que le jeu de données synthétiques, la technique d’augmentation de donnée a été intensivement utilisée. A chaque fois qu’une image est utilisée pour la backpropagation, elle est également transformée selon une liste de transformations (bruit, contraste, flip, zoom, shift, rotation, flou, couleur lunette) prédéfinie et de probabilités associées. Ce procédé peut prendre un peu de temps de calcul supplémentaire à chaque itération de gradient (calcul effectué sur CPU) mais permet au réseau d’avoir accès à des images différentes à chaque epoch et permet notamment d’éviter l’overfitting. Ces transformations et leurs probabilités sont choisies de façon arbitraire tout en veillant à ce que l’image déformée ne s’éloigne pas trop de la réalité (cf. figure [fig:data_augment]). Notez qu’il existe des techniques permettant d’apprendre une stratégie d’augmentation automatiquement par un algorithme de recherche qui trouve la meilleure stratégie en maximisant le score de validation (avec par exemple de l’apprentissage par renforcement) [autoaugment]. Cette piste a pu être évoquée mais est finalement peu recommandée pour le problème rencontré puisque le gain en performance serait minime comparé à l’effort à fournir.

Exemple d'images augmentées
Fine-Tuning
La première expérience effectuée est d’utiliser les poids pré-appris sur les données synthétiques comme initialisation pour l’entraînement sur les données réelles. Comme discuté en section [transfer_learning], il est possible d’utiliser des poids appris lors d’une tâche antérieure. Cette technique peut d’une part permettre d’accélérer l’entraînement et d’autre part améliorer les performances lorsque peu de données sont disponibles. Ici, les poids pré-appris sont utilisés comme initialisation du réseau et toutes les couches sont apprises. Trois approches sont testées : poids pré-appris sur Imagenet (Imagenet), poids pré-appris sur le jeu de données synthétiques (VTO) et poids aléatoirement initialisés (random). Comme en section [VTO_exp], l’architecture du réseau choisie est Unet. Les autres paramètres et détails d’entraînement sont également les mêmes (Dice loss, RandomSearch, learning rate constant, normalisation). La figure [fig:training_pretrained] montre l’évolution de la Loss sur les données de Test au cours de l’entraînement pour les 3 réseaux. On voit que le réseau avec les poids pré-appris sur les données synthétiques apprend très vite dès la 1ère epoch mais semble rester bloquer dans un minimum local dans les epochs suivantes. Le réseau avec poids pré-appris sur ImageNet apprend également très vite vers la 10ème epoch contrairement au réseau n’utilisant pas de poids pré-appris qui voit sa Loss descendre significativement seulement au bout de la 100ème epoch. Dans les expériences suivantes, les réseaux seront initialisés avec des poids pré-appris sur ImageNet.
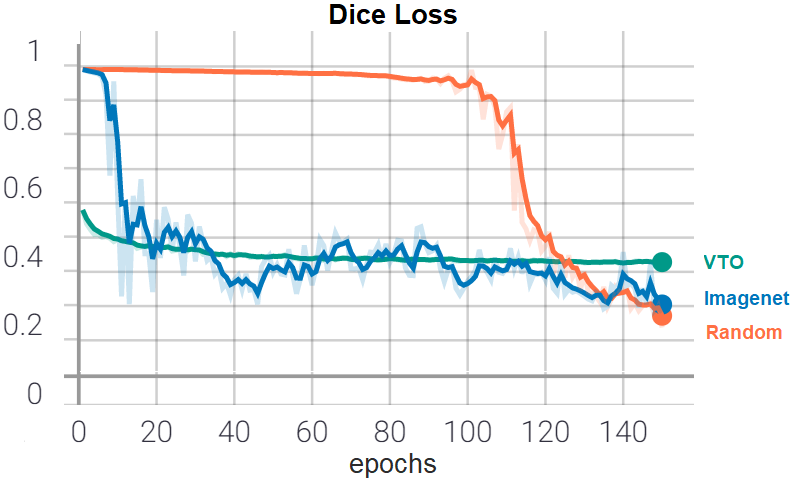
Évolution de la Dice Loss sur les données Test pour des réseaux pré-entraînés sur différents jeux de donnée.
Résolution d’images
Ensuite, la question de la taille des images pour l’entraînement a été étudiée. D’une part, parce que les temps d’entraînements peuvent être 5 fois plus lents ou plus rapides selon la taille choisie pour la configuration GPU utilisée ici. Et d’autre part, parce qu’il est possible que l’algorithme utilisant la segmentation prédite pour retrouver une position 3D nécessite une taille d’image identique à celle prise par les capteurs (à confirmer). Quatre entraînements ont été lancés dans la même configuration (architecture, optimisation, hyperparamètres) mais avec des images interpolées à des tailles différentes (cf 1ère ligne du tableau [tab:size_test]). Pour chaque entraînement, l’évaluation des performances a été faite en comparant les scores IoU moyen de trois façon différentes :
- La première est la manière classique, les images données au réseau en entrée pour l’évaluation sont à la même taille que lors de l’entraînement (ligne : Interpolation Image).
- La deuxième est d’interpoler la prédiction faite à la taille originale de l’image et de la comparer au label original (ligne : Interpolation Label).
- La troisième est d’utiliser la taille originale de l’image directement en entrée du réseau pour la prédiction (ligne : Taille originale).
Notez que l’architecture utilisée ne peut traiter que des tailles multiples de 32 dues aux différents sous-échantillonnage, sur-échantillonnage et copies des volumes. Les interpolations utilisées sont des interpolations bilinéaires peu coûteuses en temps de calcul (\textasciitilde 0.5 s). Les résultats affichées dans le tableau [tab:size_test] montrent qu’interpoler la prédiction à partir d’une image réduite fait baisser le score de 5 à 10 \% (3ème ligne du tableau) mais permet de garder un temps d’inférence par image relativement faible. Alors qu’utiliser directement la taille originale des images dans le réseau permet un gain de performance lorsque le réseau a été entraîné sur des images bien plus petites (4ème ligne du tableau). Le réseau a accès à plus d’informations et de détails dans l’image qui ont un impact important pour segmenter précisément la monture (cf. figure [fig:prediction_resolution]). En contrepartie, le temps d’inférence est plus élevé. Il est intéressant de remarquer que quelle que soit la taille d’entraînement, le modèle se généralise bien lorsqu’on lui donne en entrée une taille/résolution plus élevée pour l’inférence : par exemple on l’entraîne sur des petites images 640352 puis on prédit des images 19201056. Pour les expériences suivantes, la taille 960*544 est conservée pour éviter des entraînements trop gourmands en temps de calculs.
% on aurait aussi pu : % - se concentrer sur des architectures plus rapides comme mobilenet, bisenet (mais la taille d’entrée joue toujours sur la vitesse) % - avoir une petite image en entrée de l’encodeur mais décoder à une taille supérieur dans la dernière couche (/!\ copie Unet fonctionnerait pas) et utiliser le label plus grand que l’image d’entrée pour l’apprentissage
% \textbf{
\begin{table}[H]
\centering
\begin{tabular}{||>{\columncolor{lightgray}}m{55mm}||c|c|c|c||}
\hline
\rowcolor{lightgray} %
& (640, 352) & (960, 544) & (1280, 704) & (1600, 896)
\cline{2-5}
\rowcolor{lightgray}
\multirow{-2}{}{\diagbox{évaluation}{entraînement}} & score - temps & score - temps & score - temps & score - temps
\hline\hline
Interpolation Image & \multirow{2}{}{0.64 - 0.6} & \multirow{2}{}{0.67 - 1.7} & \multirow{2}{}{0.73 - 2.9} & \multirow{2}{}{0.74 - 4.7}
(taille entraînement) & & & &
\hline
Interpolation Label & \multirow{2}{}{0.55 - 0.7} & \multirow{2}{}{0.64 - 1.7} & \multirow{2}{}{0.67 - 2.9} & \multirow{2}{}{0.68 - 4.5}
(1280720 ou 19201080) & & & &
\hline
Taille originale & \multirow{2}{}{0.74 - 6.2} & \multirow{2}{}{0.74 - 5.5} & \multirow{2}{}{0.75 - 5.8} & \multirow{2}{}{0.75 - 5.5}
(1280704 ou 1920*1056) & & & &
\hline
\end{tabular}
\caption{Comparaison d’entraînement pour différentes résolution d’images avec les scores (IoU moyens) et les temps (inférence/image en secondes sur un CPU)}
\label{tab:size_test}
\end{table}

352*640 pixels - $IoU=46.39\%$

1920*1056 pixels - $IoU=66.96\%$
Prédiction (rouge) pour une image à 2 résolutions différentes - Modèle entraîné sur des images 352*640 pixels. Image zoomée sur la zone d'intérêt.
Architectures
Jusqu’à présent l’architecture Unet était utilisée, l’expérience suivante consiste à comparer les performances des différentes architectures énumérées en section [segmentation] : Unet, PSPNet, DeepLabV3, BiseNet. Une architecture Unet++[unet++] a également été testée, c’est une amélioration de Unet qui relie l’encodeur et le décodeur non pas avec de simples copies des sorties des couches mais avec des blocs de couches convolutionnelles. Chaque modèle est entraîné avec les mêmes paramètres et techniques d’entraînement (Dice loss, learning rate constant, normalisation, data augmentation, random search, poids pré-appris, hyperparamètres d’optimisation). La figure [fig:multiple_architectures] montrent que les architectures Unet et Unet++ atteignent un score plus élevé que les 3 autres architectures avec des scores maximum de 0.72 et 0.75 respectivement. Mon hypothèse est que les architectures BiseNet, DeepLabV3 et PSPNet ont été construites pour répondre à des problèmes multi-classes et capturer un contexte global des images sur des benchmarks connus tels que Cityscapes, PASCAL VOC ou COCO. Elles n’apportent donc pas d’amélioration pour notre problème binaire où les images sont prises suivant un protocole précis avec peu de variation de contexte global. Alors que Unet et Unet++ sont des réseaux destinés à la base pour des problèmes médicaux où l’objectif était d’avoir une segmentation la plus détaillée possible de l’image avec une seule classe présente. Finalement, l’architecture Unet est préférée pour la suite à Unet++ qui a un meilleur score mais qui est bien plus gourmande en temps de calcul.
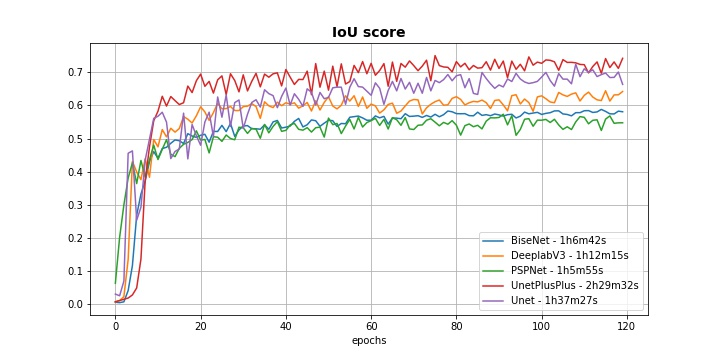
Évolution du IoU score sur les données Test pour différentes architectures
Landmarks
Une idée proposée est d’utiliser l’information des landmarks du visage pour aider le modèle à apprendre la position des lunettes. Les landmarks sont des points de repère qui sont calculés pour d’autres briques techniques du logiciel de scan 3D. Cette information étant à disposition il est possible de s’en servir pour donner une indication supplémentaire en entrée au réseau de neurones, elle encode notamment la position et l’angle de la tête du visage. Pour pouvoir utiliser ces landmarks, une carte de confiance S est générée comme recommandée pour des problèmes d’estimation de repère anatomique du corps entier [pose_estimation]. Soit $x_k$ la position du landmark $k$ dans l’image, la valeur de la carte de confiance $S_k$ associée à ce landmark $k$, en position $p$, est définie comme :
\[S_k(p) = \exp \left( -\frac{||p-x_k||^2_2}{\sigma^2} \right)\]avec $\sigma$ contrôlant l’étendu du pic. La carte de confiance générée est l’agrégation des gaussiennes de chaque landmark : $S(p) = \max_k S_k(p)$. Cette carte est ensuite concaténée à l’image RGB habituellement utilisée, le volume d’entrée n’est donc plus de taille $N_{lignes} \times N_{colonnes} \times 3$ mais est désormais de taille $N_{lignes} \times N_{colonnes} \times 4$ (cf. figure [fig:landmark_heatmap]). Avec un tel procédé, le réseau ne peut plus profiter des poids pré-appris sur ImageNet pour la 1ère couche de l’encodeur puisque les dimensions d’entrée sont différentes. De plus, le temps d’apprentissage est plus long du fait des calculs à faire sur CPU pour générer la carte de chaleur des landmarks (effectuée après chaque data augmentation).

Entrée constituée de l'image RGB et de la carte de confiance des landmarks du visage
Plusieurs modèles sont testés dans la même configuration d’entraînement mais avec différentes valeurs pour $\sigma$ (garder constant au cours de l’apprentissage). La figure [fig:multiple_sigma] ci-dessous illustre les différentes courbes d’apprentissage obtenues. Finalement, on observe que les réseaux utilisant l’information des landmarks n’obtiennent pas des performances supérieures à celui n’ayant pas l’information des landmarks en entrée. En observant les prédictions image par image, on s’aperçoit que quelque soit la position de la tête la forme globale de la monture est plutôt bien prédite. Et donc les landmarks n’apportent pas une réelle information supplémentaire pouvant être utilisée par le réseau. En réalité, les derniers pourcentages de performance manquants semblent plutôt provenir de textures, de contours proches de la monture ou parfois de caractéristiques de monture du jeu de test n’existant pas dans l’ensemble d’apprentissage. Les résultats de prédiction sont discutés en fin de section.
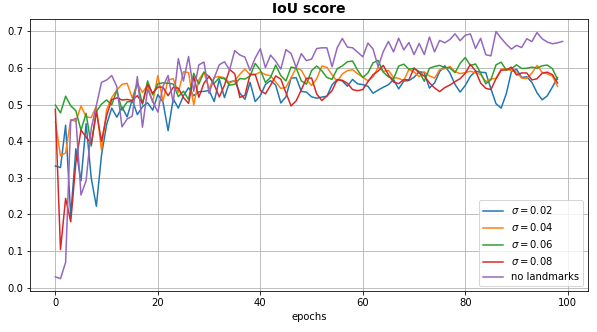
Évolution du IoU score sur les données Test pour différentes valeurs de $\sigma$
Images croppées
Finalement, une dernière expérience est d’utiliser comme image d’entrée une photo croppée, recadrée sur la zone d’intérêt. En effet, dans les expériences précédentes, l’image entière était exploitée (cf. figure [fig:nature_dataset]) alors que la zone à segmenter ne représente qu’une petite partie de l’image totale. Le choix avait été alors fait de travailler sur une image un peu moins résolue mais une approche possible est dans un premier temps de récupérer la zone de l’image où se situe la monture en utilisant soit l’information des landmarks (cf. figure [fig:cropping]) si elle est disponible soit entraîner un réseau à reconnaître grossièrement cette zone (une image basse résolution peut être utilisée pour gagner en temps de calcul). La seconde étape est alors d’entraîner le modèle de segmentation uniquement sur cette zone qui disposerait alors de la résolution maximale disponible sans être limitée par un temps de calcul excessif. L’image entière est composée de 2 millions de pixels alors que la partie représentant la monture contient environ 100 000 pixels (selon les positions). Le gain de temps est non négligeable puisque pour de telles images le temps d’inférence sur CPU est de 0.15 seconde par image (à additionner avec l’étape du cropping) contre 5 secondes pour l’image entière. Après entraînement avec une architecture Unet et un encodeur Resnet, le score final obtenu est de 0.76. On obtient comme attendu un score similaire à celui obtenu dans la dernière colonne du tableau [tab:size_test] mais on divise par 30 le temps de calcul.

Sélection de la zone d'intérêt grâce aux landmarks du visage
Résultats et Limites
Finalement, le modèle retenu est le dernier discuté qui utilise une architecture Unet avec un encodeur ResNet sur l’image croppée autour de la zone des yeux. Le score sur le jeu de test est de 0.76. Pour vérifier que la sélection du modèle n’a pas entraîné un phénomène d’overfitting, le score sur le jeu de validation est testé. Il est de 0.81. On en déduit que le modèle est bien capable de généraliser ses performances à d’autres jeux indépendants de donnée. La différence de score observée est en majorité due au fait que les jeux de données sont très petits (6 et 8 personnes) et donc que les scores de performances sont très variables. Une méthode de validation croisée pourrait être mise en place pour obtenir une estimation de performance plus précise (omise ici pour des raisons de temps de calcul).
Bien que l’objectif n’était pas de construire un modèle pour une vidéo, il est possible d’exécuter le modèle pour une suite d’image indépendamment l’une de l’autre et d’assembler ces images. La figure [fig:video_prediction] montre le résultat obtenu pour un exemple de suite d’image, on confirme visuellement que le modèle est robuste aux différentes positions du visage.
\begin{figure}[H] \centering \animategraphics[autoplay,loop,scale=0.45]{5}{Figures/animation_predictions/input_}{0}{45} \caption{Exemple de prédictions (rouge) sur une suite d’image ([mouvement_tete])} \label{fig:video_prediction} \end{figure}
On discute ici des résultats visuels des prédictions avec notamment des données du jeu de test et validation en annexe [exemples]. Globalement, la forme générale de la monture est toujours correctement prédite même pour des images où le score est entre 55 et 65 \%. Et le modèle est plutôt robuste à la diversité des montures (forme, épaisseur, textures …)
Les exemples [fig:exemple_1] et [fig:exemple_2] sont ceux qui obtiennent les scores IoU les plus élevés (86\%). Les 14\% d’erreurs restants sont des détails sur le contour de la monture et sont possiblement dus à la labellisation qui n’est pas parfaite puisque des polygones sont utilisés pour tracer le contour des montures et que l’annotateur humain ne peut pas être précis au pixel près. Les 4 images suivantes ([fig:exemple_3], [fig:exemple_4], [fig:exemple_5] et [fig:exemple_6]) illustrent la difficulté du modèle à différencier la monture des sourcils/cheveux. La variation de couleur y ait moins forte et même pour un humain il peut être difficile de distinguer précisément la frontière de la monture. Les exemples [fig:exemple_6], [fig:exemple_7] et [fig:exemple_8] caractérisent en particulier les erreurs que peut faire le modèle entre la branche, le tenon ou la charnière (cf. figure [fig:schema_lunette]). Typiquement lorsque le visage n’est pas positionné face à la caméra, la distinction entre le tenon et la charnière est difficilement perceptible surtout quand la couleur et la texture sont identiques. Enfin, les exemples [fig:exemple_9], [fig:exemple_10] et [fig:exemple_11] affichent des cas particulier où les montures possèdent une caractéristique remarquable absente dans les exemples de l’ensemble d’apprentissage comme une monture bicolore ou la monture qui se sépare en 2 parties près du nez. La prédiction est alors complètement absente à ces endroits particuliers de la monture.
Enfin le modèle a également été testé sur un ensemble de 25 images annotées provenant de Celebamask dans le but de vérifier ses performances dans un contexte différent et donc pouvoir évaluer sa robustesse aux conditions expérimentales (bruit de l’instrument, résolution, illumination, ombres). Le score IoU moyen obtenu sur cet ensemble de données est de 63\%. Un peu moins de la moitié de ces prédictions performe correctement avec un score supérieur à 75\% (cf. figure [fig:exemple_12] et [fig:exemple_13]) mais avec des contours de la monture généralement moins bien identifiés que pour la base de données utilisée pour l’entraînement. Ensuite, une partie des prédictions voit son score drastiquement diminuer en détectant faussement la branche comme faisant partie de la segmentation (cf. figure [fig:exemple_14] et [fig:exemple_15]), on peut penser que le réseau est biaisé plus vers les textures que vers les formes [texture_bias]. Le réseau peut également rencontrer des difficultés à différencier certaines ombres proches de la monture (cf. figure [fig:exemple_16]). Finalement, pour certains exemples le modèle échoue à identifier la forme globale de la monture complète (cf. figure [fig:exemple_17] et [fig:exemple_18]).
<!DOCTYPE HTML PUBLIC “-//W3C//DTD HTML 4.01 Transitional//EN”>
| [1] | Ian Goodfellow, Yoshua Bengio, and Aaron Courville. Deep Learning. MIT Press, 2016. http://www.deeplearningbook.org. [ bib ] |
| [2] | Vladimir Vapnik. Principles of risk minimization for learning theory. NIPS, 1992. [ bib ] |
| [3] | Alex Krizhevsky, Ilya Sutskever, and Geoffrey E Hinton. Imagenet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems 25, pages 1097--1105. 2012. [ bib | .pdf ] |
| [4] | Karen Simonyan and Andrew Zisserman. Very deep convolutional networks for large-scale image recognition, 2015. [ bib | arXiv ] |
| [5] | Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition, 2015. [ bib | arXiv ] |
| [6] | Olaf Ronneberger, Philipp Fischer, and Thomas Brox. U-net: Convolutional networks for biomedical image segmentation, 2015. [ bib | arXiv ] |
| [7] | Hengshuang Zhao, Jianping Shi, Xiaojuan Qi, Xiaogang Wang, and Jiaya Jia. Pyramid scene parsing network, 2017. [ bib | arXiv ] |
| [8] | Hao Li, Zheng Xu, Gavin Taylor, Christoph Studer, and Tom Goldstein. Visualizing the loss landscape of neural nets, 2018. [ bib | arXiv ] |
| [9] | James Bergstra ans Yoshua Bengio. Random search for hyper-parameter optimization. Journal of Machine Learning Research, 2012. [ bib ] |
| [10] | Jason Yosinski, Jeff Clune, Yoshua Bengio, and Hod Lipson. How transferable are features in deep neural networks? In Advances in Neural Information Processing Systems 27, pages 3320--3328. 2014. [ bib | .pdf ] |
| [11] | Y. LeCun, B. Boser, J. S. Denker, D. Henderson, R. E. Howard, W. Hubbard, and L. D. Jackel. Backpropagation applied to handwritten zip code recognition. Neural Computation, 1:541--551, 1989. [ bib ] |
| [12] | Liang-Chieh Chen, George Papandreou, Iasonas Kokkinos, Kevin Murphy, and Alan L. Yuille. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs, 2017. [ bib | arXiv ] |
| [13] | Liang-Chieh Chen, George Papandreou, Florian Schroff, and Hartwig Adam. Rethinking atrous convolution for semantic image segmentation, 2017. [ bib | arXiv ] |
| [14] | Changqian Yu, Jingbo Wang, Chao Peng, Changxin Gao, Gang Yu, and Nong Sang. Bisenet: Bilateral segmentation network for real-time semantic segmentation, 2018. [ bib | arXiv ] |
| [15] | Zongwei Zhou, Md Mahfuzur Rahman Siddiquee, Nima Tajbakhsh, and Jianming Liang. Unet++: A nested u-net architecture for medical image segmentation, 2018. [ bib | arXiv ] |
| [16] | Saining Xie, Ross Girshick, Piotr Dollár, Zhuowen Tu, and Kaiming He. Aggregated residual transformations for deep neural networks, 2017. [ bib | arXiv ] |
| [17] | Alexander Buslaev, Vladimir I. Iglovikov, Eugene Khvedchenya, Alex Parinov, Mikhail Druzhinin, and Alexandr A. Kalinin. Albumentations: Fast and flexible image augmentations. Information, 11(2), 2020. [ bib | DOI | http ] |
| [18] | Pavel Yakubovskiy. Segmentation models pytorch. https://github.com/qubvel/segmentation_models.pytorch, 2020. [ bib ] |
| [19] | Adam Paszke, Sam Gross, Francisco Massa, Adam Lerer, James Bradbury, Gregory Chanan, Trevor Killeen, Zeming Lin, Natalia Gimelshein, Luca Antiga, Alban Desmaison, Andreas Kopf, Edward Yang, Zachary DeVito, Martin Raison, Alykhan Tejani, Sasank Chilamkurthy, Benoit Steiner, Lu Fang, Junjie Bai, and Soumith Chintala. Pytorch: An imperative style, high-performance deep learning library. In H. Wallach, H. Larochelle, A. Beygelzimer, F. d Alché-Buc, E. Fox, and R. Garnett, editors, Advances in Neural Information Processing Systems 32, pages 8024--8035. Curran Associates, Inc., 2019. [ bib | .pdf ] |
| [20] | Richard Liaw, Eric Liang, Robert Nishihara, Philipp Moritz, Joseph E Gonzalez, and Ion Stoica. Tune: A research platform for distributed model selection and training. arXiv preprint arXiv:1807.05118, 2018. [ bib ] |
| [21] | Martín Abadi, Ashish Agarwal, Paul Barham, Eugene Brevdo, Zhifeng Chen, Craig Citro, Greg S. Corrado, Andy Davis, Jeffrey Dean, Matthieu Devin, Sanjay Ghemawat, Ian Goodfellow, Andrew Harp, Geoffrey Irving, Michael Isard, Yangqing Jia, Rafal Jozefowicz, Lukasz Kaiser, Manjunath Kudlur, Josh Levenberg, Dan Mané, Rajat Monga, Sherry Moore, Derek Murray, Chris Olah, Mike Schuster, Jonathon Shlens, Benoit Steiner, Ilya Sutskever, Kunal Talwar, Paul Tucker, Vincent Vanhoucke, Vijay Vasudevan, Fernanda Viégas, Oriol Vinyals, Pete Warden, Martin Wattenberg, Martin Wicke, Yuan Yu, and Xiaoqiang Zheng. TensorFlow: Large-scale machine learning on heterogeneous systems, 2015. Software available from tensorflow.org. [ bib | http ] |
| [22] | Abhishek Dutta and Andrew Zisserman. The VIA annotation software for images, audio and video. In Proceedings of the 27th ACM International Conference on Multimedia, New York, NY, USA, 2019. ACM. [ bib | DOI ] |
| [23] | Gary B. Huang, Manu Ramesh, Tamara Berg, and Erik Learned-Miller. Labeled faces in the wild: A database for studying face recognition in unconstrained environments. Technical Report 07-49, University of Massachusetts, Amherst, 2007. [ bib ] |
| [24] | Ekin D. Cubuk, Barret Zoph, Dandelion Mane, Vijay Vasudevan, and Quoc V. Le. Autoaugment: Learning augmentation policies from data, 2019. [ bib | arXiv ] |
| [25] | Zhe Cao, Tomas Simon, Shih-En Wei, and Yaser Sheikh. Realtime multi-person 2d pose estimation using part affinity fields, 2017. [ bib | arXiv ] |
| [26] | Y. Weng, T. Zhou, Y. Li, and X. Qiu. Nas-unet: Neural architecture search for medical image segmentation. IEEE Access, 7:44247--44257, 2019. [ bib | DOI ] |
| [27] | Wenming Yang, Xuechen Zhang, Yapeng Tian, Wei Wang, Jing-Hao Xue, and Qingmin Liao. Deep learning for single image super-resolution: A brief review. IEEE Transactions on Multimedia, 21(12):3106–3121, 2019. [ bib | DOI ] |
| [28] | Cheng-Han Lee, Ziwei Liu, Lingyun Wu, and Ping Luo. Maskgan: Towards diverse and interactive facial image manipulation. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2020. [ bib ] |
| [29] | Alberto Fernández Villán, Rodrigo García, Rubén Usamentiaga, and Ruben Casado. Glasses detection on real images based on robust alignment. Machine Vision and Applications, 26:1--13, 05 2015. [ bib | DOI ] |
| [30] | Bo Wu, Haizhou Ai, and Ran Liu. Glasses detection by boosting simple wavelet features. In Proceedings of the 17th International Conference on Pattern Recognition, 2004. ICPR 2004., volume 1, pages 292--295 Vol.1, 2004. [ bib | DOI ] |
| [31] | A. S. Mohammad, A. Rattani, and R. Derahkshani. Eyeglasses detection based on learning and non-learning based classification schemes. In 2017 IEEE International Symposium on Technologies for Homeland Security (HST), pages 1--5, 2017. [ bib | DOI ] |
| [32] | Shaoyi Du, Juan Liu, Yuehu Liu, Xuetao Zhang, and Jianru Xue. Precise glasses detection algorithm for face with in-plane rotation. Multimedia Systems, 23, 06 2017. [ bib | DOI ] |
| [33] | Saddam Bekhet and Hussein Alahmer. A robust deep learning approach for glasses detection in non-standard facial images. IET Biometrics, 10(1):74--86, 2021. [ bib | DOI ] |
| [34] | Geoff French, Samuli Laine, Timo Aila, Michal Mackiewicz, and Graham Finlayson. Semi-supervised semantic segmentation needs strong, varied perturbations, 2020. [ bib | arXiv ] |
| [35] | Mei Wang and Weihong Deng. Deep visual domain adaptation: A survey, 2018. [ bib | arXiv ] |
| [36] | Robert Geirhos, Patricia Rubisch, Claudio Michaelis, Matthias Bethge, Felix A. Wichmann, and Wieland Brendel. Imagenet-trained cnns are biased towards texture; increasing shape bias improves accuracy and robustness, 2019. [ bib | arXiv ] |
| [37] | Davis E. King. Dlib-ml: A machine learning toolkit. Journal of Machine Learning Research, 10:1755--1758, 2009. [ bib ] |
This file was generated by bibtex2html 1.99.