Évolution des traits d’histoires de vie de champignons phytopathogènes
Contexte
Le projet présenté ici a été réalisé dans le cadre de mon stage de M1 à l’INRIA de Sophia Antipolis.
Le projet Funfit
Ce travail s’inscrit dans le cadre du projet FUNFIT qui a commencé en octobre 2013 et qui est financé en grande partie par l’ANR, l’agence nationale de la recherche, sous forme d’un contrat de recherche à durée déterminée de 48 mois. Pour pouvoir disposer de ce financement de l’ANR s’élevant à 500 000 euros, l’équipe BIOCORE a dû répondre à un appel à projet très compétitifs (seul 10% des demandes sont financées) et convaincre l’ANR en présentant les enjeux et objectifs du projet FUNFIT dont la problématique générale est de mieux comprendre l’évolution des champignons pathogènes des arbres forestiers grâce à la mise en relation entre expériences biologiques et les biomathématiques dans le but de réduire l’impact des maladies sur les écosystèmes. Les champignons sont à l’origine de nombreuses maladies chez les plantes, en agriculture et dans les écosystèmes naturels. Dans le contexte des changements écologiques actuels, les champignons ont été identifiés comme la cause majeure des nouvelles maladies des plantes, notamment dues à l’introduction d’espèces qui étaient jusqu’alors absentes dans certaines régions. En effet, les champignons ont un fort impact négatif sur le rendement des cultures et causent une réelle perte à la récolte. La compréhension de cet environnement épidémiologique est donc un enjeu majeur qui nécessite le développement de méthodes permettant de prédire l’évolution de ces organismes pathogènes. Ces dernières années, de nombreuses études ont été menées sur ce sujet d’un point de vue de la génétique des populations et de la génomique. Le projet FUNFIT se place dans un cadre conceptuel liant l’évolution des traits des champignons phytopathogènes* pour faire le lien entre fitness** individuelle et stratégies écologiques. Le projet a pour objectif d’apporter une contribution dans ce domaine en construisant un cadre théorique focalisé sur les traits d’histoire de vie***, incluant schémas et modèles et en s’appuyant sur un travail expérimental portant sur quelques espèces représentatives de champignons pathogènes forestiers. Le projet repose sur le fait que la caractérisation des traits d’histoire de vie chez les champignons phytopathogènes permettra de mieux cerner l’origine du succès évolutif d’un champignon pathogène ainsi que la dynamique des populations de champignons pathogènes, et donc l’impact des maladies des plantes dans les écosystèmes naturels. L’ensemble des résultats acquis apportera une contribution à la connaissance de l’écologie des champignons et à la gestion des maladies forestières. Globalement, le projet FUNFIT a pour but de contribuer à la compréhension de la façon dont les champignons évoluent dans les conditions changeantes de l’environnement et comment exploiter cette connaissance pour réduire l’impact négatif que portent ces champignons sur les cultures d’arbre.
* Qualifie un organisme vivant susceptible d’infecter les végétaux et d’y déclencher des maladies.
** Concept central en théorie de l’évolution qui décrit la capacité d’un individu d’un certain génotype à se reproduire. Peut-être mesurée par exemple par le nombre de descendants atteignant la maturité sexuelle.
*** Ensemble des caractéristiques d’un individu contribuant à sa fitness dans un milieu donné. Ils reflètent donc l’adaptation d’un organisme à survivre à son environnement
La rouille du peuplier
Trois maladies majeures des arbres forestiers ont été retenues comme modèles d’étude pour le projet FUNFIT : la rouille du peuplier, le chancre du châtaignier et l’oïdium du chêne. Le sujet de mon stage porte sur le champignon appelé Melampsora larici-populina responsable de la rouille du peuplier. C’est un champignon parasite qui infecte les arbres notamment les peupliers et semble dans certains cas (ex : monocultures) pouvoir déjouer les défenses immunitaires naturelles des arbres. Les conséquences infectieuses de ce champignon sont l’affaiblissement la culture, c’est-à-dire une croissance réduite et une plus forte sensibilité aux autres maladies. Pour une souche donnée de Melampsora, il existe de fortes différences de sensibilité des souches de peuplier à ce champignon, mais le champignon qui dans la nature coévolue avec ses hôtes se trouve ici face à des milliers de clones dans le cadre de monocultures. Ceci impose une forte pression de sélection sur les champignons : seuls ceux ayant la capacité de contourner les résistances naturels de l’arbre peuvent subsister dans un environnement où ils sont alors sans concurrence. Le champignon parasite peut alors rapidement déjouer les défenses de son hôte potentiel. L’INRA*, en France, a déjà produit plusieurs souches et clones de peupliers initialement déclarées résistants à la rouille, mais la rouille du peuplier s’est montrée capable d’évoluer rapidement par le jeu des mutations. Ce champignon s’est ainsi rapidement propagé dans les cultures de peupliers (dans toute la France, il y a plusieurs décennies), alors qu’il fait peu de dégâts chez les peupliers sauvages. Dans les années 1990, à la suite cette diffusion de clones peu variés de peupliers auxquels il s’est adapté dès 1994, il a fait d’importants dégâts (allant de forte défoliation** avec retards de croissance à la mort des arbres). Ayant évolué, il s’est montré capable d’infecter la plupart des cultivarNBé pour analyser la dynamique de croissance de ces champignons. L’objectif du stage sera d’exploiter ce modèle qui permettrait d’identifier si une des deux stratégies identifiées précédemment peut être le résultat de l’évolution à long terme de l’espèce, en tenant compte de divers facteurs : la limitation de la ressource, la compétition entre les pathogènes, voire la saisonnalité.

Échantillon d'une feuille infectée par la rouille du peuplier
* Institut national de la recherche agronomique.
** Phénomène de pertes de tout ou une partie des feuilles d’un arbre souvent dues à des maladies, parasites ou insectes.
*** Variété de plante obtenue en culture qui a été sélectionnée pour ses caractéristiques uniques.
La dynamique adaptative
L’objectif de l’étude est d’exploiter des modèles mathématiques et des résultats existants 1 2 pour identifier s’il existe une stratégie qui pourrait être le résultat de l’évolution à long terme de l’espèce grâce à la théorie de la dynamique adaptative. C’est une théorie qui est apparue petit à petit dans les années 1990 en combinant des outils déjà existant comme la théorie des jeux évolutionnaires 3 et la dynamique des populations 4 afin d’obtenir une dynamique eco-évolutive réaliste. En effet, cette théorie est un outil très utilisé en biologie qui tente d’expliquer les liens entre différents mécanismes comme l’hérédité, les mutations et la sélection naturelle. Elle permet de comprendre le lien entre évolution et démographie et notamment de visualiser et de comprendre la conséquence à long terme de petites mutations d’un trait au sein d’une population et est donc très utile pour modéliser les scénarios évolutifs. Les hypothèses à respecter sont les suivantes :
- Le mutant est rare quand il apparaît ce qui nous permet de dire que sa densité est négligeable.
- La modification du trait mutant est légère par rapport au trait du résident.
- Les individus se reproduisent de façon clonale.
- Les populations sont à l’équilibre écologique lorsqu’un mutant apparaît car le taux de mutation est très faible. Ceci implique que deux mutants ne peuvent exister en même temps ni au même endroit.
Le but est d’observer le devenir de ce mutant rare dans la population. Soit il disparaît, soit il envahit le milieu. En envahissant le milieu le mutant devient le nouveau résident en changeant la valeur d’un trait phénotypique le caractérisant qui lui permet d’avoir une meilleure fitness (taux de croissance) que le résident. Excepté dans le cas des branchement évolutifs où les populations mutantes et résidentes sont stables et ont toutes les deux un taux de croisssance positifs, elles peuvent coexister et créer ainsi deux populations avec des traits différents (ce qui pourrait expliquer le phénomène de spéciation).
Afin de respecter l’hypothèse sur la faible densité du mutant, dans les simulations on se place dans le cas où $n_1 = 100$ (taille de la population résidente) et $n_2 = 1$ (taille de la population mutante).
Le modèle - 1 cohorte
La modèlisation mathématique présenté après s’appuie sur ce qu’il se passe au niveau biologique lors de l’infection. En effet, l’infection se déroule en 3 étapes : la pénétration dans la feuille, la croissance du mycélium (ensemble filamenteux du champignon qui permet d’absorber les ressources nécessaires à la survie et à la croissance du champignon) et enfin la sporulation.

Représentation du cycle biologique de Melampsora
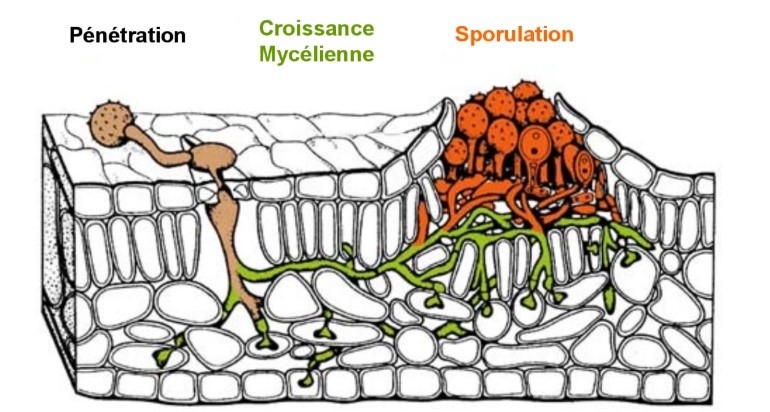
Schéma de coupe d'une infection par Melampsora sur l'épiderme d'une feuille
Pour développer le modèle, il a été considéré que le champignon choisissait sa stratégie soit pour maximiser la quantité de spores (cellule issue de la reproduction) produites au cours de son existence soit pour s’assurer qu’une souche proche ne pourra pas exploiter la stratégie qu’il aurait choisi pour produire plus de spores que lui. On considère une cohorte de champignons se développant pendant une saison sur une même plante hôte et on s’intéresse à la densité de la lésion notée $n$ et représentant la quantité de mycélium dans la cohorte par unité d’aire de l’hôte, on suppose que $n$ est constant pendant la saison. D’où, le modèle suivant :
\[\left\{ \begin{array}{ll} \frac{dM(t)}{dt} = (1-u(t)).f(M(t))-g(M(t)) \\ \frac{dS(t)}{dt} = u(t).\delta .f(M(t)) \\ M(0) = M_0 , S(0) = S_0 \\ 0 \leqslant u(t) \leqslant 1, t \in [0,T] \end{array} \right. \text{ avec } \left. \begin{array}{ll} f(M) = \frac{\alpha M}{M+\kappa}.\frac{1}{1+\beta nM} \\ g(M) = \gamma M \\ \end{array} \right.\] 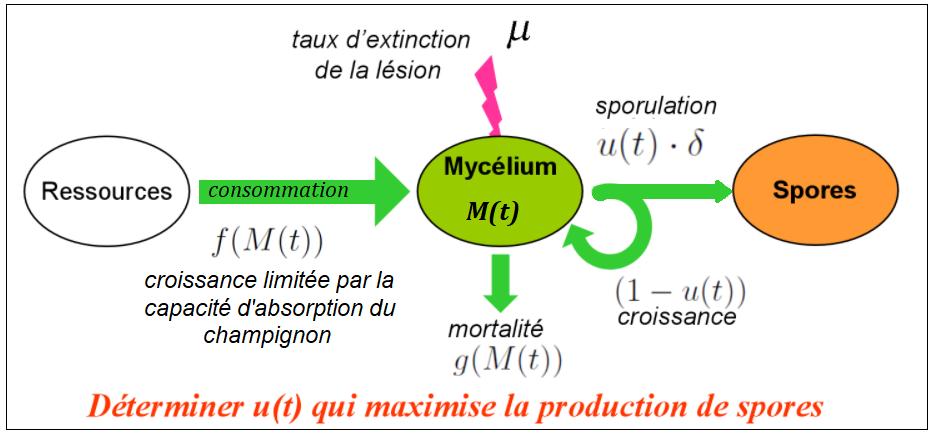
Cadre théorique du modèle
On représente ici sous forme d’équations différentielles ordinaires (EDO) l’évolution au cours du temps des quantités $M$ et $S$ qui sont respectivement la taille moyenne du mycélium et la quantité moyenne de spores à un instant t de la saison. Cependant, il faut savoir que comme le membre de droite dans la 2ème équation ne contient pas $S(t)$ nous n’avons pas besoin de traiter explicitement $S(t)$, c’est à dire que $M(t)$ peut être considéré comme la seule variable d’état. Les fonctions $f$ et $g$ sont des fonctions représentant le taux de croissance et de mortalité du mycélium, la fonction $f$ comprend un facteur représentant le flux de ressource qui peut être obtenu par une hyphe, c’est-à-dire une branche du mycélium et un autre facteur qui est l’influence négative de la compétition entre les hyphes du champignon. La variable $u$ correspond à un terme d’allocation des ressources compris entre 0 et 1. Quand $u(t) = 0$, toutes les ressources sont utilisées pour la croissance du mycélium et quand $u(t) = 1$, les ressources sont entièrement consacrées à la production de spores. La constante $\delta$ est le rendement de la production de spores en comparaison de celle du mycélium. La variable de temps $t$ joue le rôle de l’âge de l’infection. Il faut savoir qu’on peut se placer dans 2 cas pour cette étude, lorsque la dynamique du champignon est assez rapide par rapport à la durée totale de la saison on peut considérer que l’intervalle observé est $\left[0;+\infty\right[$ , si ce n’est pas le cas alors on se place sur un intervalle fini $\left[0;T\right]$ . Dans le cas d’un intervalle infini, le problème est de déterminer $u(t)$ qui maximisera la quantité de spores à la fin de la saison, sachant le champignon doit réussir à répartir de la bonne manière ses ressources entre la production de spores (= reproduction, i.e la survie de l’espèce) et la production de mycélium (organe qui absorbe les ressources). Ce problème revient à trouver le $u(t)$ qui maximise la quantité $\int_0^T \frac{dS(t)}{dt} e^{-\mu t} \, dt$ avec un terme exponentiel prenant en compte $\mu$ le taux d’extinction de la cohorte de champignons sur la feuille (si par exemple la feuille est arrachée de l’arbre). Ce facteur $e^{-\mu t}$ indique une importance moindre des spores produites aux temps élNBevés car il est fort probable qu’à ces temps-là la lésion n’existe plus. Un tel problème d’optimalité a été résolu grâce au principe du maximum de Pontryagin 1 et permet d’arriver au résultat que
\[u(M) = \left\{ \begin{array}{ll} 0, M < M^* \\ 1, M > M^* \\ u^*, M = M^* \\ \end{array} \right. \text{ avec } \left\| \begin{array}{ll} M^* \text{ tel que } f'(M^{*})-g'(M^{*}) = \mu \\ u^* = 1 - \frac{g(M^*)}{f(M^*)} \end{array} \right.\]Dans le cas d’un intervalle fini, l’étude développée par 1 et qui s’appuie sur la résolution de l’équation d’Hamilton Jacobi Bellman (issue de la théorie de la programmation dynamique, et utilise une méthode dites des caractéristiques) conclut alors qu’il est nécessaire de construire une surface de commutation représentée par :
\[\lambda = \left\{(t,M) \in [0,T]\times]0,M^{*}] : \lambda(T-t,M) = 0 \right\} \text{ avec } \left\| \begin{array}{ll} \lambda(\tau,M)=-\int_0^\tau e^{-(\gamma+\mu)s}f'(Me^{-\gamma s})ds+1 \\ \tau = T-t \end{array} \right.\]Dans ce cas, d’un point de vue biologique, c’est comme ci à partir d’un certain moment donné avant la fin de la saison le champignon concentrait toutes ces ressources à produire uniquement des spores et c’est compréhensible puisque on sait que des stress initiateurs comme des changements de saison (le début de l’hiver par exemple) peuvent être à l’origine de la fructification chez de nombreuses espèces de champignons. La commande $u$ est alors définie par
\[u(t,M) = \left\{ \begin{array}{ll} 0, M<M^{*}, \lambda(\tau,M) \geqslant 0 \\ 1, M>M^{*}, \lambda(\tau,M) < 0 \\ u^*, M=M^* , 0 \leqslant t < T - \tau^* \\ 1, M>M^* \end{array} \right. \text{ avec } \left\| \begin{array}{ll} M^* \text{ tel que } f'(M^*)-g'(M^*) = \mu \\ u^* = 1 - \frac{g(M^*)}{f(M^*)} \\ \tau^* \text{ tel que } \lambda(\tau^*,M^*)=0 \end{array} \right.\]La 1ère étape du travail a été de simuler ce modèle sur Scilab. Pour obtenir cette première simulation, la fonction $\textcolor{blue}{ode()}$ prédéfinie de Scilab qui est un solveur d’équations différentielles ordinaires explicite du 1er ordre et utilise la méthode Runge-Kutta par défaut peut être exploité. Le paramètre “stiff” est adapté au problème présenté ici puisqu’il permet de résoudre des systèmes raides et utilise le schéma BDF (Backward Differentiation Formula), ici on a bien un système raide dû au fait que $\dot{M}$ varie fortement entre $ M < M^* $ et $ M > M^* $ pendant un temps très court.

Simulation du système dynamique - modèle 1 cohorte (n=100). A gauche, le cas où on considère un intervalle infini et à droite, un intervalle fini
Le modèle - 2 cohortes
L’enjeu de l’étude qui a été menée par l’équipe BIOCORE était d’étendre ce modèle dynamique à la théorie des jeux évolutionnaires puisque cela permettrait de décrire un possible équilibre évolutif dans des situations réalistes où plusieurs cohortes pathogènes sont en compétition pour une ressource commune parmi une plante hôte. En effet, la théorie des jeux évolutifs est une branche particulière de la théorie des jeux développée par des biologistes de l’évolution à partir des années 1970 3 qui permet de décrire les stratégies utilisées par des populations d’individus et de déterminer quelles sont les stratégies stables du point de vue de l’évolution et définir des équilibres biologiques ; bien qu’optimale, la stratégie décrite précédemment n’est en effet peut-être pas imbattable car elle pourrait être exploitée par un mutant adoptant une autre stratégie. Ainsi, il a été considéré 2 cohortes de champignons sur la même plante hôte et, en partant du modèle à 1 cohorte précédent, développé le sytème suivant :
\[\left\{ \begin{array}{ll} \frac{dM_1(t)}{dt} = (1-u_1(t)).f_1(M_1(t),M_2(t))-g(M_1(t)) \\ \frac{dM_2(t)}{dt} = (1-u_2(t)).f_2(M_1(t),M_2(t))-g(M_2(t)) \\ \frac{dS_1(t)}{dt} = u_1(t).\delta .f_1(M_1(t),M_2(t)) \\ \frac{dS_2(t)}{dt} = u_2(t).\delta .f_2(M_1(t),M_2(t)) \\ M_1(0)=M_1^0 , M_2(0)=M_2^0 , S_1(0)=S_1^0 , S_2(0)=S_2^0 \\ 0 \leqslant u_1(t) \leqslant 1, 0 \leqslant u_2(t) \leqslant 1, t \in [0,T] \end{array} \right. \text{ avec } \left\| \begin{array}{ll} f_i(M_1,M_2) &= \frac{\alpha M_i}{M_i+\kappa}.\frac{1}{1+\beta (n_1M_1+n_2M_2)} \\ g(M) &= \gamma M \end{array} \right.\]La fitness de chaque cohorte peut être écrite comme :
\[J_i(u_1,u_2) = \int_0^T u_i(t)f_i(M_1(t),M_2(t))e^{-\mu t} dt\longrightarrow\underset{u_i(.)}{\sup}\]L’équation dynamique d’état et le critère d’optimisation correspondant sont maintenant remplacés par 2 équations dynamique d’état et leur critère d’invasion. Dans les deux équations et leur critère de fitness, on a un terme de compétition qui apparaît et qui dépend des 2 variables d’état. En appliquant la théorie des jeux et la théorie du contrôle à ce modèle, de nombreux résultats intéressants ont été trouvés dans l’étude 2 notamment l’existence d’une stratégie évolutionnairement stable (ESS) c’est-à-dire qu’une cohorte voulant envahir ne pourra pas trouver de stratégie lui permettant de produire plus de spores2. Le jeu résultant est défini par le système d’équation précédent et le critère $J_1 - J_2 \longrightarrow \underset{u_1}{\sup} ~ \underset{u_2}{\inf}$ car chaque cohorte essaie d’avoir une meilleure fitness individuelle que l’autre. Cela définira une stratégie non invasible.
La solution de ce jeu ressemble à celle du problème de commande optimale au détail près que le niveau singulier $M^{*}$ est supérieur à $M^$.

Simulation du système dynamique - modèle 2 cohortes, n=10 et T=30 d'après
La question qu’on se pose dans ce travail est de savoir si cet équilibre non invasible obtenu par la théorie des jeux sera bien le résultat de l’évolution telle que défini par la dynamique adaptative.
Travail réalisé
Le problème dans le modèle développé dans notre exemple est que nous n’avons pas d’expression explicite de la taille de nos populations (ici $n_1$ et $n_2$), nous ne pouvons pas faire une étude analytique du modèle avec la théorie de la dynamique adaptative. Mon travail était donc de simuler avec Scilab numériquement en confrontant chaque stratégie 2 à 2 les unes après les autres. Une stratégie l’emporte sur une autre si ses gains sur la durée sont supérieurs à ceux de l’autre stratégie. En biologie, les gains d’un individu sont directement mesurables par le nombre de ses descendants. Le terme stratégie est lié aux traits d’histoire de vie mentionnés plus haut, dans notre modèle c’est la taille moyenne de mycélium que va essayer d’atteindre le champignon pendant sa croissance qu’on appellera $M^{\sigma}$ \label{trait} et pour le cas d’un intervalle fini, un autre trait se rajoute c’est le temps $\tau^{\sigma}$ qu’on peut qualifier comme le moment auquel le champignon décide d’utiliser toutes ses ressources à ne produire que des spores avant la fin de la saison. La stratégie non invasible qui a été mise en évidence par les travaux précédents est de choisir comme valeur de trait un \(M^{**}\) qui vérifie \(f'(M^{**})-g'(M^{**}) = \mu\) et un \(\tau^{**}\) tel que \(\lambda(\tau^{**},M^{**}) = 0\).
Etude à 1 trait - $T=+\infty$
Diagramme PIP
On s’intéresse d’abord au cas où l’on considère un intervalle de temps infini qui est plus simple car on étudie un seul trait, $M^\sigma$, et on suppose que le nombre total de lésions $n$ était constant d’une année à l’autre mais pas la répartition entre les cohortes. On simule donc la compétition au cours de plusieurs saisons de 2 cohortes de champignons ayant adoptées des stratégies proches mais différentes et à chaque fin de saison $i$ la densité de lésion de la première cohorte $n_1$ est recalculée en utilisant $n_1^{i+1} =\frac{n_1^i. J_1^i}{n_1^i. J_1^i+n_2^i. J_2^i} n$ (de la même façon pour $n_2$). Le produit $n_1^i J_1^i$ représente le nombre de spores produites à la fin de la saison $i$ par toute la cohorte 1 et $n_1^i. J_1^i+n_2^i. J_2^i$ le nombre total de spores produites par les deux cohortes. Ainsi pour obtenir $n_1^{i+1}$ on multiplie la proportion de spores produits par la cohorte 1 par rapport à la production totale des 2 cohortes par la quantité $n = n_1+n_2$. On constate qu’au bout de plusieurs saisons, l’une des cohortes de champignon tend à disparaître (sauf si les 2 cohortes ont la même stratégie) comme on peut le voir sur la figure ci-dessous.
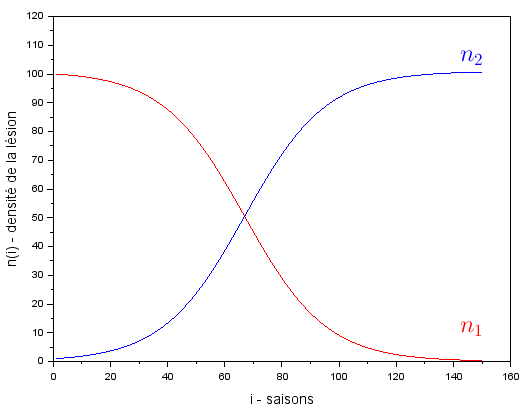
Exemple de l'évolution de $n_1$ et $n_2$ (pour $M_1^\sigma = 1250$ et $M_2^\sigma = 1750$)
La cohorte restante est celle qui aura choisi une meilleure stratégie, elle devient la population résidente et est comparée ensuite à une autre stratégie (mutante) proche choisie aléatoirement pour respecter les hypothèses de la dynamique adaptative, par exemple dans le code Scilab on utilise : $ M_m^\sigma = M_r^\sigma+\epsilon*(rand()-0.5)$ \footnote{Pour simplifier les notations par la suite pour parler du trait $M^\sigma$ d’une façon population mutante ou résidente on utilisera souvent $M_r$ et $M_m$ au lieu de $M^\sigma_r$ ou $M^\sigma_m$ (idem pour le trait $\tau^\sigma$), ils possèdent cependant la même signification.}, ça signifie que la valeur du trait $M^\sigma$ de la population mutante est choisie aléatoirement dans l’intervalle $[M^\sigma_r-\frac{\epsilon}{2};M^\sigma_r+\frac{\epsilon}{2}]$. On recommence ce processus jusqu’à se rendre compte que l’on converge vers une stratégie qui gagne à tous les coups et est donc imbattable. On remarque que ce $M^\sigma$ stable est très proche du $ M^{**} $. \label{dynstochM}
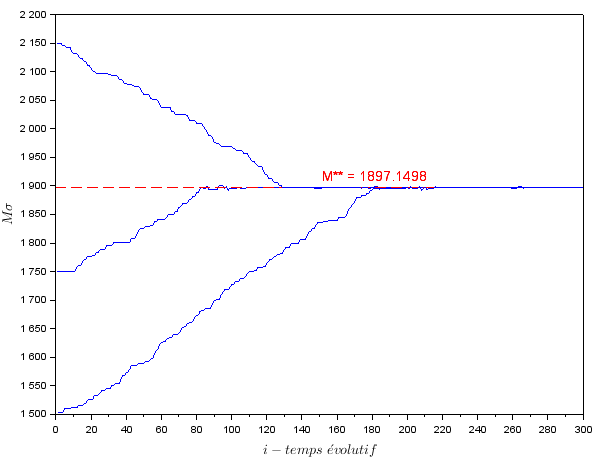
Convergence stochastique vers $ M^{**} $ en partant de conditions initiales différentes ($M^\sigma_0 = 1500, 1750 \text{ et } 2150$)
A partir de là, un outil graphique connu en théorie de la dynamique adaptative appelé le diagramme d’invasion binaires ou PIP (Pairwise Invasibility Plots)quireprésente en abscisse la valeur du trait de la population résidente et en ordonnée la valeur du trait de la population mutante. Ici les points rouges représente les cas où le mutant peut envahir la population résidente et les points bleu le cas contraire. Le PIP trouvé nous donne 2 résultats significatifs :
- le point singulier semble bien correspondre à $M^\sigma = M^{**}$ et donc être le même que celui trouvé dans 2.
- en choississant n’importe quelles valeurs de trait initiales, on converge vers cet équilibre stable donc c’est une stratégie continûment stable (CSS).
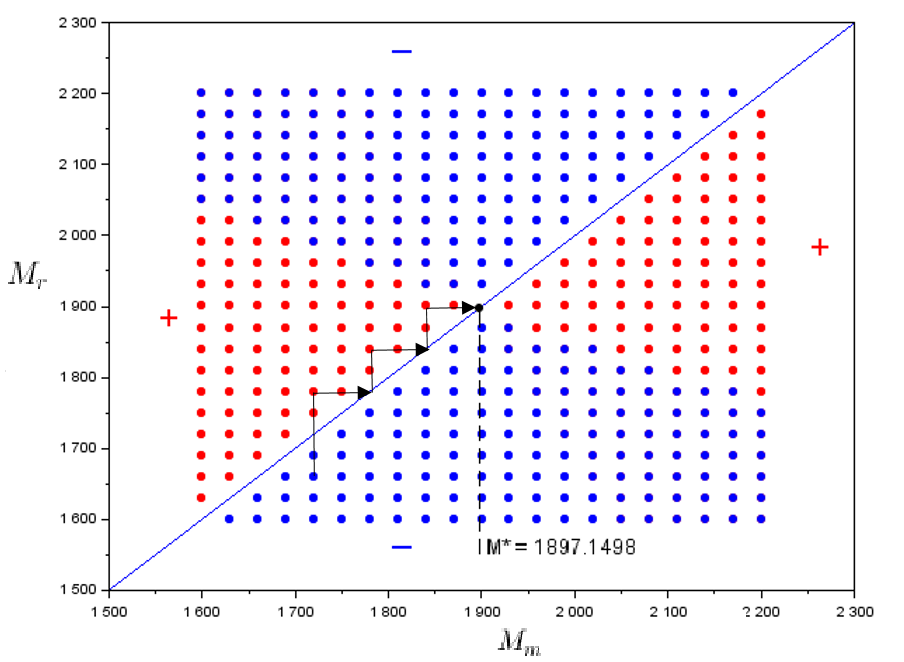
diagramme PIP
Caractérisation du point singulier
Exposant d’invasion
En dynamique adaptative, une grandeur qui est régulièrement utilisée est l’exposant d’invasion, il est défini comme le taux de croissance d’un mutant dans un environnement en majorité occupé par des résidents et mesure donc la capacité d’un mutant à envahir et remplacer une population résidente. A chaque invasion réussie par un mutant, le trait phénotypique étudié du résident est remplacé par le trait du mutant comme en théorie des jeux évolutifs mais en plus avec un processus d’optimisation vers une meilleure fitness de la population. Dans le cas de tailles de populations définies par des dynamiques continus, on peut calculer cet exposant d’invasion en utilisant
\[s(M_r,M_m) = \lim\limits_{n_m \to 0} \frac{\dot{n}_m}{n_m} \text{ avec } \left\| \begin{array}{ll} M_r : \text{trait des résidents} \\ M_m : \text{trait des mutants} \\ n_m : \text{taille de la population mutante} \\ n_r : \text{taille de la population résidente} \end{array} \right.\]On peut appliquer cette formule dans des cas analytiques quand $\dot{n}_m$ et $n_m$ sont explicités, ce qui n’est pas le cas ici. Numériquement, pour le cas discret, on va calculer :
\[s(M_r,M_m) = log \left( \frac{n_m(1)}{n_m(0)} \right) \text{ avec } \left\| \begin{array}{ll} n_m(1): \textrm{taille de la population mutante après une seule saison} \\ n_m(0): \text{taille de la population mutante initiale (petite)} \end{array} \right.\]Cependant, on peut se demander si le fait de regarder l’évolution sur seulement une saison avec une petite population mutante donne une bonne approximation de l’évolution des populations au long terme après plusieurs saisons. En superposant, le diagramme PIP précédemment obtenu, dans lequel on regardait si vraiment les mutants remplaçaient les résidents sur le long terme, à un contour plot de la fonction s, on s’aperçoit que les deux coïncident : le comportement sur la 1ère saison est le même que celui le long du temps évolutif. En effet, lorsque $s$ est positif alors $n_m(1) > n_m(0) $, la population mutante augmente d’une saison à l’autre (contour plot) et elle remplace les résidents (points bleus). Quand $s$ est négatif alors $n_m(1) < n_m(0) $, la population mutante diminue par rapport à la saison précédente, elle n’envahit pas.
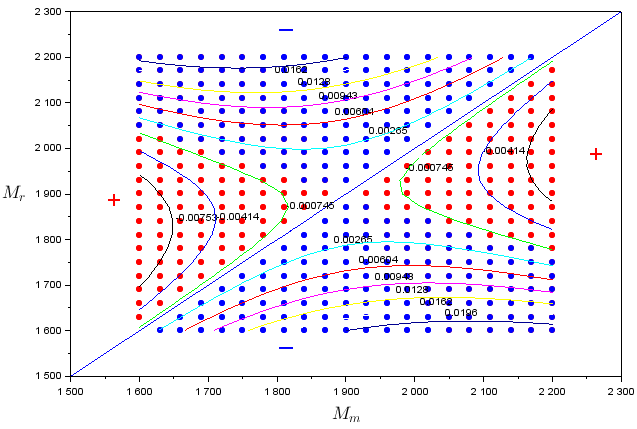
Exposant d'invasion
Gradient de sélection
On définit le gradient de sélection comme la variation de l’exposant d’invasion au point $m = r$, c’est à dire qu’il quantifie la vitesse à laquelle le trait varie et dans quelle direction. Numériquement, on fait une approximation en calculant une dérivée numérique centrée (ordre 2).
\[\left.\frac{\partial s}{\partial M_m} \right| _{M_m=M_r} \simeq \frac{s(M_r,M_r+h)-s(M_r,M_r-h)}{2h} \quad \text{, avec h petit}\]En regardant son signe, on peut connaître le comportement du trait et notamment si l’on se trouve à un point singulier de l’évolution 5 :
- si \(\left.\frac{\partial s}{\partial M_m} \right| _{M_m=M_r} > 0\) alors le trait augmente.
- si \(\left.\frac{\partial s}{\partial M_m} \right| _{M_m=M_r} < 0\) alors le trait diminue.
- si \(\left.\frac{\partial s}{\partial M_m} \right| _{M_m=M_r} = 0\) alors on est à un point singulier de l’évolution.

Gradient de sélection - 1 trait
On remarque que notre gradient de sélection calculé numériquement s’annule logiquement en un $M^\sigma \simeq M^{**}$. On a donc trouvé, numériquement, un point singulier de l’évolution et on peut le caractériser grâce aux propriétés concernant la dynamique adaptative 6 comme suit :
- si \(\left.\frac{\partial^2s}{\partial {M_m}^2} \right| _{M_m=M_r=M^{**}} < 0\) alors \(M^{**}\) est une stratégie évolutivement stable (ESS), les mutants avec une stratégie proche ne peuvent pas envahir.
- si \(\left.\frac{\partial^2s}{\partial {M_m}^2} \right| _{M_m=M_r=M^{**}} < \left.\frac{\partial^2s}{\partial {M_r}^2} \right| _{M_m=M_r=M^{**}}\) alors \(M^{**}\) est stable par convergence, si les résidents ont une stratégie $ M^\sigma $ proche de $ M^{**} $ alors les mutants ayant réussit à envahir sont encore plus proche de la stratégie \(M^{**}\).
- si \(\left.\frac{\partial^2s}{\partial {M_m}^2} \right| _{M_m=M_r=M^{**}} et \left.\frac{\partial^2s}{\partial {M_r}^2} \right| _{M_m=M_r=M^{**}} > 0\) alors les mutants et les résidents peuvent potentiellement coexister, on parle de point de branchement si l’équilibre est stable.
Dans notre cas, on calcule les dérivées secondes numériques, c’est-à-dire :
\[\left.\frac{\partial^2s}{\partial M_m^2} \right| _{M_m=M_r=M^{**}} \simeq \frac{s(M^{**},M^{**}+h)-2s(M^{**},M^{**})+s(M^{**},M^{**}-h)}{h^2} = -4,464.10^{-10} \\ \left.\frac{\partial^2s}{\partial M_r^2} \right| _{M_m=M_r=M^{**}} \simeq \frac{s(M^{**}+h,M^{**})-2s(M^{**},M^{**})+s(M^{**}-h,M^{**})}{h^2} = 5,551.10^{-19}\]On trouve que notre point singulier \(M^{**}\) vérifie les conditions pour être ESS et stable par convergence. On dit alors que \(M^{**}\) est une stratégie continûment stable (CSS). L’évolution tend à faire converger le trait $M^\sigma$, la taille moyenne du mycélium à atteindre durant la saison du champignon Melampsora, vers la stratégie non invasible \(M^{**}\).
Etude à 2 traits - $T<+\infty$
Pour le cas d’un intervalle de temps fini, il y a deux traits qui peuvent évoluer, $M^\sigma$ et $\tau^\sigma$. Nous ne pouvons donc pas afficher le PIP puisqu’il faudrait 2$\times$2 dimensions. Cependant, il n’est pas impossible de se rendre compte de ce qu’il se passe en traçant les stratégies gagnantes dans le plan $(\tau^\sigma;M^\sigma) $ en simulant une dynamique sochastique, de la même façon que pour le cas à 1 trait, comme suit :
\[\left\{ \begin{array}{ll} M_m^\sigma &=& M_r^\sigma+\epsilon_M*(rand()-0.5) \\ \tau_m^\sigma &=& \tau_r^\sigma+\epsilon_\tau*(rand()-0.5) \end{array} \right.\]Et en partant de conditions initiales différentes on obtient plusieurs trajectoires qui convergent vers le même point : la stratégie non invasible $ (M^{},\tau^{}) $ (voir figure ci-dessous).

Convergence stochastique vers $ (M^{**},\tau^{**}) $ avec $\epsilon_M=10$ et $\epsilon_\tau = 0.2$
Dans ce cas à 2 traits, on peut aussi utiliser l’exposant d’invasion $s(M_r,M_m,\tau_r,\tau_m)$ comme pour le cas à 1 trait mais celui-ci a désormais 4 arguments (contre 2 avant) et le gradient de sélection est de dimension 2, on peut le calculer numériquement de cette façon :
\[\left.\frac{\partial s}{\partial M_m} \right| _{(M_m,\tau_m) = (M_r,\tau_r)} \simeq \frac{s(M_r,\tau_r,M_r+h_M,\tau_r)-s(M_r,\tau_r,M_r-h_M,\tau_r)}{2h_M} \\ \left.\frac{\partial s}{\partial \tau_m} \right| _{(M_m,\tau_m) = (M_r,\tau_r)} \simeq \frac{s(M_r,\tau_r,M_r,\tau_r+h_\tau)-s(M_r,\tau_r,M_r,\tau_r-h_\tau)}{2h_\tau}\]Pour trouver notre point singulier, on affiche le niveau 0 de ces 2 fonctions et on regarde leur point d’intersection. On constate qu’il y a un seul point singulier dont on voudrait savoir s’il est stable et attractif.
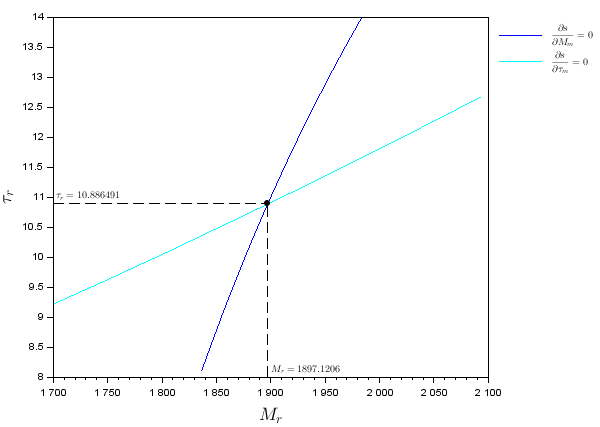
Gradients de sélection - 2 traits
Caractérisation du point singulier
Les gradients de sélection calculés numériquement s’annulent en même temps en un point singulier de l’évolution qui est \((M^{**},\tau^{**})\). Pour le caractériser, on utilise les résultats sur la stabilité des points singuliers à plusieurs traits 78 qui ont été formulé par Leimar comme suit :
Soit $x$ le vecteur des traits des résidents et $x’$ le vecteur des traits des mutants, on définit J la matrice Jacobienne du gradient de sélection et H la Hessienne de l’exposant d’invasion tel que
\[\mathrm{J}_{jk} = \left.\frac{\partial^2s(x',x)}{\partial x'_j\partial x'_k}\right| _{x'=x=x^*}+\left.\frac{\partial^2s(x',x)}{\partial x'_j\partial x_k}\right| _{x'=x=x^*} \text{ et ~~~~~~ } \mathrm{H}_{jk} = \left.\frac{\partial^2s(x',x)}{\partial x'_j\partial x'_k}\right| _{x'=x=x^*}\]- si $J$ est définie négative alors le point $x^*$ est stable par convergence.
- si $H$ et $J$ sont définies négatives alors le point $x^*$ est CSS.
- si $H$ est indéfinie ou définie positive et J est définie négative alors $x^*$ est un point de branchement évolutif.
En adaptant ces résultats et ces notations à notre cas, on a :
\[\begin{array}{ll} \mathrm{J} = \left.\begin{pmatrix} \frac{\partial^2s}{\partial {M_m}^2}+\frac{\partial^2s}{\partial M_m\partial M_r} & \frac{\partial^2s}{\partial M_m\partial \tau_m}+\frac{\partial^2s}{\partial M_m\partial \tau_r} \\ \frac{\partial^2s}{\partial \tau_m\partial M_m}+\frac{\partial^2s}{\partial \tau_m\partial M_r} & \frac{\partial^2s}{\partial {\tau_m}^2}+\frac{\partial^2s}{\partial \tau_m\partial \tau_r} \end{pmatrix}\right| _{\binom{M_m}{\tau_m}=\binom{M_r}{\tau_r}=\binom{M^{**}}{\tau^{**}}} \\ \mathrm{H} = \left.\begin{pmatrix} \frac{\partial^2s}{\partial {M_m}^2} & \frac{\partial^2s}{\partial M_m\partial \tau_m} \\ \frac{\partial^2s}{\partial \tau_m\partial M_m} & \frac{\partial^2s}{\partial {\tau_m}^2} \end{pmatrix}\right| _{\binom{M_m}{\tau_m}=\binom{M_r}{\tau_r}=\binom{M^{**}}{\tau^{**}}} \end{array}\]On approxime ces dérivées du second ordre numériquement en utilisant des différences finies centrées :
\[\begin{array}{ll} \left.\frac{\partial^2s}{\partial {M_m}^2} \right| _{\binom{M_m}{\tau_m}=\binom{M_r}{\tau_r}=\binom{M^{**}}{\tau^{**}}} \simeq \frac{s(M^{**},\tau^{**},M^{**}+h_M,\tau^{**})-2s(M^{**},\tau^{**},M^{**},\tau^{**})+s(M^{**},\tau^{**},M^{**}-h_M,\tau^{**})}{h_M^2} \end{array} \\ \begin{array}{ll} \left.\frac{\partial^2s}{\partial {\tau_m}^2} \right| _{\binom{M_m}{\tau_m}=\binom{M_r}{\tau_r}=\binom{M^{**}}{\tau^{**}}} \simeq \frac{s(M^{**},\tau^{**},M^{**},\tau^{**}+h_\tau)-2s(M^{**},\tau^{**},M^{**},\tau^{**})+s(M^{**},\tau^{**},M^{**},\tau^{**}-h_\tau)}{h_\tau^2} \end{array}\]Les dérivées mixtes sont calculées en utilisant l’approximation suivante :
\[\frac{\partial^2}{\partial x \partial y}f(x,y) \simeq \frac{f(x+h,y+k)-f(x+h,y-k)-f(x-h,y+k)+f(x-h,y-k)}{4hk}\]On obtient les matrices de la figure ci-dessous, qui sont toutes les deux définies négatives car toutes leurs valeurs propres sont strictement négatives (det>0 et tr<0). Notre point singulier est CSS. On en conclut qu’au fil de l’évolution, les traits $(M^\sigma,\tau^\sigma)$ du champignon Melampsora tendent à converger vers la stratégie non invasible \((M^{**},\tau^{**})\).
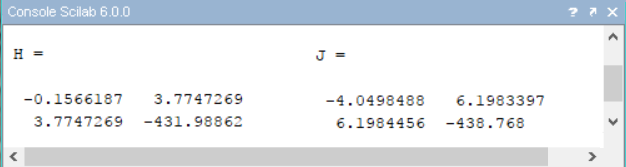
Calcul numérique des matrices J et H (à un facteur $10^6$ près)
Équation canonique
Dieckmann et Law 9 ont développé une équation pour représenter la trajectoire d’une façon déterministe des mutations et portant le nom d’équation canonique.
\[\frac{d}{dt}x = m(x).C(x).\left.\frac{\partial s}{\partial x'}\right| _{x'=x} \text{ avec } \left\| \begin{array}{ll} x : \text{vecteur des traits résidents} \\ x': \text{vecteur des traits mutants} \\ m : \text{potentiel évolutif de la mutation} \\ C : \text{matrice de covariance} \\ \end{array} \right.\]Dans notre cas, on étudie les 2 traits $M^\sigma$ et $\tau^\sigma$ et on considère qu’ils évoluent tous les deux de manières indépendantes donc la matrice de covariance est diagonale, notre équation canonique s’écrit alors
\[\left\{ \begin{array}{ll} \frac{d}{dt}M_r &=& \theta_M .\left.\frac{\partial s}{\partial M_m}\right| _{M_r=M_m} \\ \frac{d}{dt}\tau_r &=& \theta_\tau .\left.\frac{\partial s}{\partial \tau_m}\right| _{\tau_r=\tau_m} \end{array} \right.\]En codant cet ODE sur Scilab, on obtient la figure suivante et on voit bien que peu importe la condition initiale que l’on choisit, on converge bien vers \((M^*,\tau^*)\) ce qui confirme bien nos résultats obtenus précédemment de manière stochastique.

Simulation de l'équation canonique avec $\theta_M = 2500$ et $\theta_\tau = 1$
On superpose ensuite nos résultats obtenus de façon déterministe et stochastique. Cependant, il faut faire attention aux coefficients devant chaque équations, si l’on veut que les 2 graphiques soient cohérents. Les équations qui régissent l’évolution des traits sont :
\[\begin{align*} \underline{stochastique} &: \left\{ \begin{array}{ll} M_m^\sigma &=& M_r^\sigma+\epsilon_M*(rand()-0.5) \\ \tau_m^\sigma &=& \tau_r^\sigma+\epsilon_\tau*(rand()-0.5) \end{array} \right. \\ \\ \underline{déterministe} &: \left\{ \begin{array}{ll} \frac{d}{dt}M_r &=& \theta_M .\left.\frac{\partial s}{\partial M_m}\right| _{M_r=M_m} \\ \frac{d}{dt}\tau_r &=& \theta_\tau .\left.\frac{\partial s}{\partial \tau_m}\right| _{\tau_r=\tau_m} \end{array} \right. \end{align*}\]Dans l’équation canonique (déterministe), les coefficients représentent la variance de nos traits. Or, on utilise la fonction $\textcolor{blue}{rand()}$ de Scilab (stochastique) comme une loi uniforme continue $U(a,b)$ dont la variance est $\frac{(b-a)^2}{12}$, ce qui veut dire que les variances de $M_m^\sigma$ et $\tau_m^\sigma$ sont $\frac{\epsilon_M^2}{12}$ et $\frac{\epsilon_\tau^2}{12}$ respectivement. Pour rester cohérents, il faut alors que nos coefficients vérifient la relation $\frac{\epsilon_M^2}{\epsilon_\tau^2}=\frac{\theta_M}{\theta_\tau}$. Dans notre cas, on choisit $\frac{\epsilon_M}{\epsilon_\tau}=\frac{10}{0.2}=50$ et $\frac{\theta_M}{ \theta_\tau}= \frac{2500}{1}$ pour respecter cette condition. On constate alors que les simulations stochastiques et déterministes sont cohérentes.
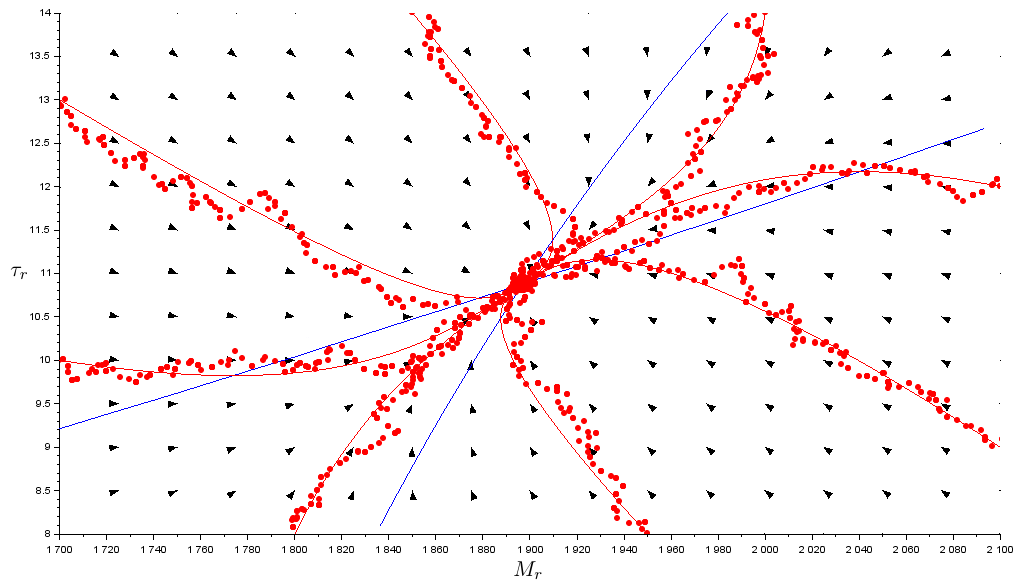
Superposition des résultats déterministe et stochastique
Compromis évolutif (trade-off)
Le compromis évolutif est un concept récurrent en biologie évolutive, en effet les contraintes énergétiques exigent qu’un gain dans une zone de l’histoire de vie d’une espèce est obtenu au prix d’une perte dans un autre domaine. Par exemple, il existe des individus développant des résistances à certaines maladies mais entraînant des effets secondaires indésirables d’où le nom de compromis. On a donc souhaité explorer la potentielle existence d’un compromis évolutif entre nos 2 traits $M^\sigma$ et $\tau^\sigma$. En exprimant le trait $\tau^\sigma$ en fonction du trait $M^\sigma$ on peut mettre en place ce compromis évolutif et passer d’une étude de 2 traits à une étude à 1 trait. Pour trouver cette fonction, on affiche les couples \((M^{**};\tau^{**})\) obtenus dans 2 en fonction des paramètres $\gamma$ et $\mu$ qui sont les paramètres biologiques principaux liés à la mortalité et à la croissance de nos individus. Ensuite, on cherche la meilleure courbe quadratique qui approxime ce nuage de point en utilisant la méthode des moindres carrés.
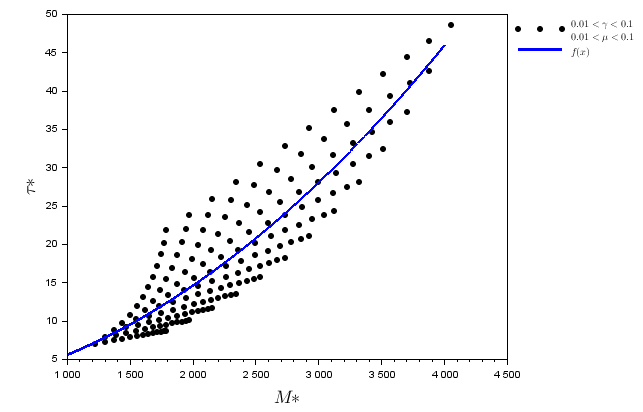
Compromis évolutifs
Le compromis évolutif reliant \(M^{**}\) et \(\tau^{**}\) s’écrit alors \(\tau^{**} = a.{M^{**}}^2+b.{M^{**}}+c\) avec $a = 0.0000022$, $b = 0.002406$ et $c = 0.9991782$. Bien qu’il n’y ait pas de base biologique à ce compromis, on constate qu’il représente assez bien le lien entre \(M^{**}\) et \(\tau^{**}\) dans le cas où les paramètres $\gamma$ et $\mu$ sont variables. On l’impose donc et on obtient une analyse plus simple. Maintenant qu’on a une relation entre \(M^{**}\) et \(\tau^{**}\), on peut calculer le gradient de sélection comme pour le cas à 1 trait et voir quand il s’annule pour trouver le point singulier.
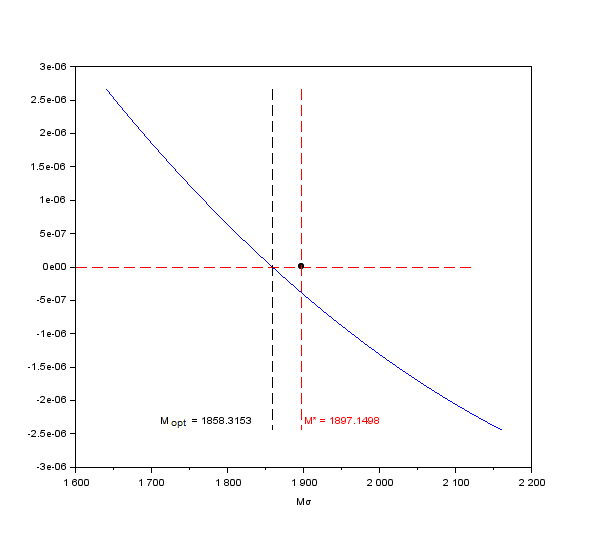
Gradient de sélection avec compromis évolutifs
On remarque que ce point singulier n’est pas tout à fait atteint en \(M^{**}\) la stratégie non invasible à cause de la mise en place du compromis.
Discussion
En conclusion, les simulations numériques réalisées ont confirmé la stabilité et l’attractivité de l’équilibre d’un point de vue de l’évolution au long terme pour les cas à 1 traits et à 2 traits. On a cohérence avec les travaux 2, mais on peut se demander si nos résultats sont toujours valables en augmentant le nombre de trait jusqu’à un cadre plus abstrait où l’on étudierait une infinité de traits.
References
-
Yegorov, Y., Grognard, F., Mailleret, L., Halkett , F. Optimal resource allocation for biotrophic phatogens. IFAC World Congress, Toulouse, 2017 ↩ ↩2 ↩3
-
Yegorov, Y., Grognard, F., Mailleret, L., Halkett, F., Bernhard, P. A dynamic game approach to uninvadable strategies for biotrophic pathogens. en préparation Sophia-Antipolis, 2017 ↩ ↩2 ↩3 ↩4 ↩5 ↩6 ↩7
-
John Maynard Smith, Evolution and the Theory of Games. United Kingdom, 1982, 234 pages ↩ ↩2
-
Beverton, R.J.H., Holt, S.J. On the dynamics of exploited fish populations, 1957, 538 pages ↩
-
Diekmann, O., A beginner’s guide to adaptive dynamics. Banach Center Publication 2004, 63 ↩
-
Brännström, A., Johansson, J., Festenberg, N. The Hitchhiker’s guide to adaptive dynamics. Games 2013, 4, p. 304-328 ↩
-
Leimar, O., The Evolution of Phenotypic Polymorphism: Randomized Strategies versus Evolutionary Branching. The American Naturalist 2005, 165, p. 669-681 ↩
-
Leimar, O., Multidimensional convergence stability. Evolutionnary Ecology Research 2009, 11, p.~191-208 ↩
-
Dieckmann, U., Law, R., The dynamical theory of coevolution : a derivation from stochastic processes. Journal of Mathematical Biology 1996, 34, p. 579-612 ↩